Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan]

Pembahasan soal Ujian Nasional (UN) SMA-IPA bidang studi Matematika dengan materi pembahasan Sistem Pertidaksamaan Linear yang meliputi:

• daerah sistem pertidaksamaan linear dan 
• model matematika sistem pertidaksamaan linear.

Konsep 1

Untuk menentukan persamaan garis dari suatu grafik, gunakan konsep berikut ini!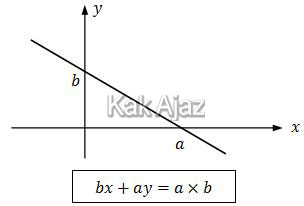

Konsep 2

Untuk menentukan daerah pertidaksamaan, gunakan konsep berikut ini!

Soal No. 1 tentang Daerah Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

Daerah yang memenuhi sistem pertidaksamaan linear x + y ≤ 4; x + 4y ≥ 8, x ≥ 0, y ≥ 0 adalah ….

A.	I
B.	II
C.	III
D.	IV
E.	V

Pembahasan

Berdasarkan konsep pengerjaan soal nomor 2 maka: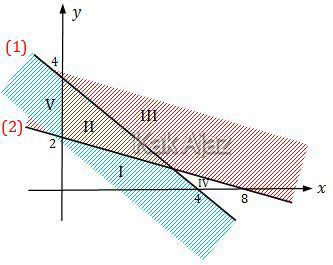

Pertidaksamaan (1) adalah x + y ≤ 4. Karena tanda pertidaksamaannya “≤” maka daerah yang diarsir berada di bawah garis (arsiran biru).

Sedangkan pertidaksamaan (2) adalah x + 4y ≥ 8. Karena tanda pertidaksamaannya “≥” maka daerah yang diarsir berada di atas garis (arsiran merah).

Sementara itu, arsiran warna coklat merupakan irisan pertidaksamaan (1) dan (2) di kuadran I (x ≥ 0, y ≥ 0).

Jadi, daerah yang memenuhi sistem pertidaksamaan linear adalah daerah II (B).

Soal No. 2 tentang Daerah Sistem Pertidaksamaan Linear

Daerah yang memenuhi sistem pertidaksamaan linear 3x + 4y ≤ 96; x + y ≤ 30; x ≥ 0; y ≥ 0 adalah ….

A.	I
B.	II
C.	III
D.	IV
E.	V

Pembahasan

Kedua pertidaksamaan di atas bertanda “≤” sehingga dapat dipastikan daerah pertidaksamaan keduanya berada di bawah garis.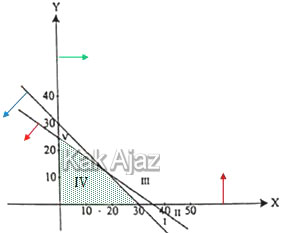

Sementara itu, sistem pertidaksamaan tersebut berada di kuadran pertama (x ≥ 0, y ≥ 0).

Jadi, daerah yang memenuhi sistem pertidaksamaan linear tersebut adalah daerah IV (D).

Soal No. 3 tentang Model Matematika Sistem Pertidaksamaan Linear

Daerah yang diarsir pada gambar di bawah ini adalah daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan ….

A.	x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0
B.	x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0
C.	x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0
D.	x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0
E.	x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0

Pembahasan

Perhatikan gambar berikut ini!

Daerah arsiran pada grafik di atas dibatasi oleh garis (1), garis (2), dan garis (3).

Garis (1) dan daerah arsiran di bawahnya:

4x + 4y ≤ 16
    x + y ≤ 4

Garis (2) dan daerah arsiran di atasnya:

2x + 5y ≥ 10

Garis (3) atau garis x = 0 (sumbu y) dan daerah di sebelah kanannya:

x ≥ 0

Jadi, daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan opsi (C).

Soal No. 4 tentang Model Matematika Sistem Pertidaksamaan Linear

Daerah yang diarsir pada gambar di bawah ini adalah daerah penyelesaian dari pertidaksamaan ….

A.	6x + y ≤ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0
B.	6x + y ≥ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0
C.	6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0
D.	6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0
E.	x + 6y ≤ 12; 4x + 5y ≥ 20; x ≥ 0; y ≥ 0

Pembahasan

Perhatikan grafik di bawah ini!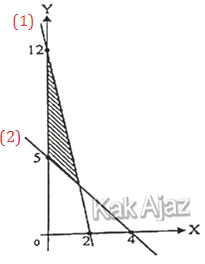

(1)   12x + 2y = 24
(2)   5x + 4y = 20

Persamaan garis (1) perlu disederhanakan, sedangkan persamaan (2) sudah dalam bentuk yang paling sederhana. Sehingga,

(1)   6x + y = 12
(2)   5x + 4y = 20

Daerah yang diarsir terletak di sebelah kiri garis (1) dan di atas garis (2). Tanda pertidaksamaan untuk daerah sebelah kiri adalah “≤” sedangkan daerah atas adalah “≥” . Diperoleh:

(1)   6x + y ≤ 12
(2)   5x + 4y ≥ 20

Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.

x ≥ 0; y ≥ 0

Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (A).

Soal No. 5 tentang Model Matematika Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

Daerah yang diarsir pada gambar di atas merupakan daerah penyelesaian dari sistem pertidaksamaan ….

A.	x + 2y ≥ 8; 2x + 3y ≥12; x ≥ 0; y ≥ 0
B.	2x + y ≥ 8; 3x + 2y ≥ 12; x ≥ 0; y ≥ 0
C.	2x + y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0
D.	2x + y ≤ 8; 3x + 2y ≤ 12; x ≥ 0; y ≥ 0
E.	x + 2y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0

Pembahasan

Perhatikan gambar berikut ini!

(1)   8x + 4y = 32
(2)   4x + 6y = 24

Jika kedua persamaan di atas disederhanakan maka akan menjadi:

(1)   2x + y = 8
(2)   2x + 3y = 12

Daerah yang diarsir terletak di bawah garis (1) dan di bawah garis (2) sehingga tanda pertidaksamaannya adalah “≤” (kurang dari atau sama dengan).

(1)   2x + y ≤ 8
(2)   2x + 3y ≤ 12

Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.

x ≥ 0; y ≥ 0

Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (C).

Simak juga:
Pembahasan Matematika IPA UN: Sistem Persamaan Linear 
Pembahasan Matematika IPA UN: Program Linear

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.