Soal tentang Luas Daerah UN 2014
Luas daerah arsiran pada gambar dapat dinyatakan dengan rumus ….

A. 0∫2 [(7 − x) − (x2 − 2x + 1)] dx
B. 0∫3 [(7 − x) − (x2 − 2x + 1)] dx
C. 0∫2 [(x2 − 2x + 1) − (7 − x)] dx
D. 0∫3 [(x2 − 2x + 1) − (7 − x)] dx
E. 0∫1 (x2 − 2x + 1) dx + 1∫3 (7 − x) dx

A. 0∫2 [(7 − x) − (x2 − 2x + 1)] dx
B. 0∫3 [(7 − x) − (x2 − 2x + 1)] dx
C. 0∫2 [(x2 − 2x + 1) − (7 − x)] dx
D. 0∫3 [(x2 − 2x + 1) − (7 − x)] dx
E. 0∫1 (x2 − 2x + 1) dx + 1∫3 (7 − x) dx
Pembahasan
Secara keseluruhan, daerah yang diarsir pada gambar di atas dibatasi oleh:sumbu y : x = 0
garis : y1 = 7 − x
kurva : y2 = x2 − 2x + 1
Adapun batas x, sebelah kiri dibatasi oleh sumbu y atau x = 0 dan sebelah kanan dibatasi oleh titik potong antara garis dan kurva, yaitu x = 3. Batas x ini akan menjadi batas integrasi.
x1 = 0 dan x2 = 3
Sedangkan batas y, sisi atas dibatasi oleh garis y1 dan sisi bawah dibatasi oleh kurva y2. Batas y ini digunakan untuk menentukan fungsi yang akan diintegral, yaitu fungsi atas dikurangi fungsi bawah.
y1 − y2
Dengan demikian, luas daerah yang diarsir dirumuskan:
L = x1∫x2 (y1 − y2) dx
= 0∫3 [(7 − x) − (x2 − 2x + 1)] dx
Jadi, luas daerah arsiran pada gambar dapat dinyatakan dengan rumus pada opsi (B).
Soal tentang Luas Daerah UN 2013
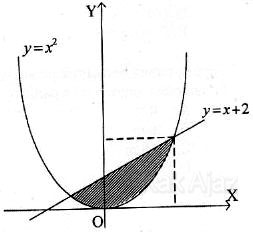
Luas daerah yang diarsir pada gambar dapat dinyatakan dengan rumus ….
A. L = −1∫2 (x + 2 + x2) dx
B. L = −1∫2 (x − 2 − x2) dx
C. L = −1∫2 (x + 2 − x2) dx
D. L = −2∫1 (−x + 2 + x2) dx
E. L = −2∫1 (−x + 2 + x2) dx

A. L = −1∫2 (x + 2 + x2) dx
B. L = −1∫2 (x − 2 − x2) dx
C. L = −1∫2 (x + 2 − x2) dx
D. L = −2∫1 (−x + 2 + x2) dx
E. L = −2∫1 (−x + 2 + x2) dx

Pembahasan
Pada gambar di atas, batas integrasinya merupakan titik potong antara kurva y1 = x2 dan garis y2 = x + 2. Titik potong kurva dan garis tersebut dapat dicari dengan cara menyamakan kedua fungsi tersebut.y1 = y2
x2 = x + 2
x2 − x − 2 = 0
(x + 1)(x − 2) = 0
x1 = −1 dan x2 = 2
Sisi atas daerah yang diarsir dibatasi oleh garis y2 = x + 2 dan sisi bawah dibatasi oleh kurva y1 = x2. Sehingga fungsi yang akan diintegral adalah:
y2 − y1
Dengan demikian, luas daerah yang diarsir dirumuskan:
L = x1∫x2 (y2 − y1) dx
= −1∫2 [(x + 2) − x2 ] dx
= −1∫2 (x + 2 − x2) dx
Jadi, luas daerah yang diarsir pada gambar tersebut dapat dinyatakan dengan rumus pada opsi (C).
Soal tentang Luas Daerah UN 2011
Luas daerah yang dibatasi kurva y = 4 − x2, y = −x + 2, dan 0 ≤ x ≤ 2 adalah ….
A. 8/3 satuan luas
B. 10/3 satuan luas
C. 14/3 satuan luas
D. 16/3 satuan luas
E. 26/3 satuan luas
A. 8/3 satuan luas
B. 10/3 satuan luas
C. 14/3 satuan luas
D. 16/3 satuan luas
E. 26/3 satuan luas
Pembahasan
Luas daerah tersebut berada pada interval 0 ≤ x ≤ 2. Artinya, daerah tersebut dibatasi x1 = 0 dan x2 = 2.Sekarang perhatikan kurva y1 = 4 − x2. Kurva tersebut terbuka ke bawah (karena koefisien x2-nya negatif). Karena terbuka ke bawah maka posisinya pasti ada di atas.
Perhatikan gambar berikut!

Pada daerah arsiran, y1 berada di atas y2 sehingga:
y1 − y2 = 4 − x2 − (−x + 2)
= 4 − x2 + x − 2
= −x2 + x + 2
Dengan demikian, luas daerah yang diarsir adalah:

Sekarang kita masukkan batas-batasnya. Batas x = 0 tidak perlu dimasukkan karena pasti akan menghasilkan nol.
= −1/3∙23 + 1/2∙23 + 2∙2
= −8/3 + 2 + 4
= −8/3 + 6
= −8/3 + 18/3
= 10/3
Jadi, luas daerah yang dimaksud adalah 10/3 satuan luas (B).
Soal tentang Luas Daerah UN 2012
Luas daerah yang dibatasi oleh kurva y = x2 + 3x + 4 dan y = 1 − x adalah ….
A. 2/3 satuan luas
B. 4/3 satuan luas
C. 7/4 satuan luas
D. 8/3 satuan luas
E. 15/3 satuan luas
A. 2/3 satuan luas
B. 4/3 satuan luas
C. 7/4 satuan luas
D. 8/3 satuan luas
E. 15/3 satuan luas
Pembahasan
Batas integrasi daerah tersebut adalah titik potong antara kurva y1 = x2 + 3x + 4 dan garis y2 = 1 − x.Mari kita cari titik potong tersebut.
y1 = y2
x2 + 3x + 4 = 1 − x
x2 + 4x + 3 = 0
(x + 3)(x + 1) = 0
x1 = −3 dan x2 = −1
Kurva y1 terbuka ke atas (karena koefisien x2-nya positif), berarti posisi kurva y1 berada di bawah garis y1. Sehingga fungsi yang diintegral adalah:
y2 − y1 = 1 − x − (x2 + 3x + 4)
= 1 − x − x2 − 3x − 4)
= −x2 − 4x − 3
Dengan demikian, luas daerah yang dimaksud adalah:
Selanjutnya kita masukkan batas-batasnya.
= −1/3 (−1 − (−27)) − 2(1 − 9) − 3(−1 − (−3))
= −26/3 + 16 − 6
= −26/3 + 10
= −26/3 + 30/3
= 4/3
Jadi, luas daerah yang dimaksud adalah 4/3 satuan luas (B).
Soal tentang Luas Daerah UN 2015
Luas daerah yang dibatasi oleh kurva y = −x3 + x2 + 6x dan sumbu x adalah ….
A. 20 7/12 satuan luas
B. 21 1/12 satuan luas
C. 21 5/12 satuan luas
D. 21 7/12 satuan luas
E. 22 5/12 satuan luas
A. 20 7/12 satuan luas
B. 21 1/12 satuan luas
C. 21 5/12 satuan luas
D. 21 7/12 satuan luas
E. 22 5/12 satuan luas
Pembahasan
Kita tentukan dulu titik potong antara kurva y1 = −x3 + x2 + 6x dan sumbu x atau y2 = 0.y1 = y2
−x3 + x2 + 6x = 0
x3 − x2 − 6x = 0
x(x2 − x − 6) = 0
x(x + 2)(x − 3) = 0
x = 0, x = −2, dan x = 3
Grafik kurva tersebut dapat digambarkan sebagai berikut:

Daerah yang diarsir pada gambar di atas terbagi menjadi dua. Artinya, untuk mendapatkan luas daerah tersebut kita harus melakukan integral dua kali.
Luas daerah pertama, sebut saja L1, berada di antara x = −2 dan x = 0. Daerah L1 bernilai negatif karena berada di bawah sumbu x.
Untuk itu, perlu kita kalikan negatif sebelumnya atau batasnya kita tukar agar bernilai positif.

Batas x = 0 tidak perlu dimasukkan karena pasti akan menghasilkan nol.
= −1/4 (−2)4 + 1/3 (−2)3 + 3(−2)2
= −4 − 8/3 + 12
= 8 − 8/3
= 24/3 − 8/3
= 16/3
= 5 1/3
Sedangkan daerah yang kedua, sebut saja L2, berada di antara x = 0 dan x = 3.
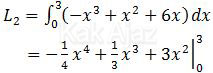
Dengan hanya memasukkan betas x=3 diperoleh:
= −1/4∙34 + 1/3∙33 + 3∙32
= −81/4 + 9 + 27
= 36 − 81/4
= 144/4 − 81/4
= 63/4
= 15 3/4
Dengan demikian, luas seluruh daerah tersebut adalah:
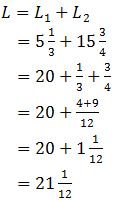
Jadi, luas daerah tersebut adalah 21 1/12 satuan luas (B).
Pembahasan soal Luas Daerah yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 34
Pembahasan Matematika IPA UN 2014 No. 34
Pembahasan Matematika IPA UN 2015 No. 36
Pembahasan Matematika IPA UN 2016 No. 35
Simak juga, Pembahasan Matematika IPA UN: Volume Benda Putar [Aplikasi Integral]
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.


No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan