
Pembahasan soal-soal Ujian Nasional (UN) bidang studi Matematika SMA-IPA dengan materi pembahasan Lingkaran yang meliputi:
- persamaan lingkaran,
- persamaan garis singgung lingkaran.
Soal tentang Lingkaran UN 2013
Persamaan lingkaran yang berpusat pada titik (4, −3) dan berdiameter 8 cm adalah ….
A. x2 + y2 − 8x + 6y = 0
B. x2 + y2 + 8x − 6y + 16 = 0
C. x2 + y2 − 8x + 6y + 16 = 0
D. x2 + y2 + 8x − 6y + 9 = 0
E. x2 + y2 − 8x + 6y + 9 = 0
A. x2 + y2 − 8x + 6y = 0
B. x2 + y2 + 8x − 6y + 16 = 0
C. x2 + y2 − 8x + 6y + 16 = 0
D. x2 + y2 + 8x − 6y + 9 = 0
E. x2 + y2 − 8x + 6y + 9 = 0
Pembahasan
Persamaan lingkaran dengan pusat (x1, y1) dan jari-jari r dirumuskan:(x − x1)2 + (y − y1)2 = r2
Berdasarkan rumus di atas, persamaan lingkaran dengan pusat (4, −3) dan diameter 8 (jari-jari 4) adalah:
(x − 4)2 + (y + 3)2 = 42
x2 − 8x + 16 + y2 + 6y + 9 = 16
x2 + y2 − 8x + 6y + 9 = 0
Jadi, persamaan lingkaran yang berpusat pada titik (4, −3) dan berdiameter 8 cm adalah opsi (E).
Soal tentang Lingkaran UN 2015
Persamaan lingkaran yang berpusat di titik (1, −3) dan menyinggung garis x + 2y + 10 = 0 adalah ….
A. x2 + y2 − 2x + 6y + 5 = 0
B. x2 + y2 − 2x − 6y + 5 = 0
C. x2 + y2 + 2x + 6y + 5 = 0
D. x2 + y2 − 2x + 6y + 15 = 0
E. x2 + y2 + 2x + 6y + 15 = 0
A. x2 + y2 − 2x + 6y + 5 = 0
B. x2 + y2 − 2x − 6y + 5 = 0
C. x2 + y2 + 2x + 6y + 5 = 0
D. x2 + y2 − 2x + 6y + 15 = 0
E. x2 + y2 + 2x + 6y + 15 = 0

Pembahasan
Jarak antara titik pusat lingkaran (x1, y1) terhadap garis singgung ax + by + c = 0 merupakan jari-jari lingkaran tersebut yang dirumuskan:
Sehingga jari-jari yang berpusat di titik (1, −3) dan menyinggung garis x + 2y + 10 = 0 adalah:

Dengan demikian, persamaan lingkaran tersebut adalah:
(x − x1)2 + (y − y1)2 = r2
(x − 1)2 + (y + 3)2 = (√5)2
x2 − 2x + 1 + y2 + 6y + 9 = 5
x2 + y2 − 2x + 6y + 5 = 0
Jadi, persamaan lingkaran tersebut adalah opsi (A).
Soal tentang Lingkaran UN 2011
Persamaan garis singgung lingkaran
x2 + y2 − 6x + 4y − 12 = 0 di titik (7, 1) adalah ….
A. 3x − 4y − 41 = 0
B. 4x + 3y − 55 = 0
C. 4x − 5y − 53 = 0
D. 4x + 3y − 31 = 0
E. 4x − 3y − 40 = 0
x2 + y2 − 6x + 4y − 12 = 0 di titik (7, 1) adalah ….
A. 3x − 4y − 41 = 0
B. 4x + 3y − 55 = 0
C. 4x − 5y − 53 = 0
D. 4x + 3y − 31 = 0
E. 4x − 3y − 40 = 0
Pembahasan
Persamaan garis singgung lingkaran dalam bentuk x2 + y2 + Ax + By + C = 0 di titik (x1, y1) dirumuskan sebagai:x1 x + y1 y + ½A(x1 + x) + ½B(y1 + y) + C = 0
Dengan demikian, persamaan garis singgung lingkaran x2 + y2 − 6x + 4y − 12 = 0 di titik (7, 1) adalah:
7x + 1y − 3(7 + x) + 2(1 + y) − 12 = 0
7x + y − 21 − 3x + 2 + 2y − 12 = 0
4x + 3y − 31 = 0
Jadi, persamaan garis singgung lingkaran tersebut adalah opsi (D).
Soal tentang Lingkaran UN 2014
Persamaan garis singgung pada lingkaran 2x2 + 2y2 + 4x − 8y − 8 = 0 yang sejajar dengan garis 5x + 12y − 15 = 0 adalah ….
A. 5x + 12y − 20 = 0 dan 5x + 12y + 58 = 0
B. 5x + 12y + 20 = 0 dan 5x + 12y − 58 = 0
C. 5x + 12y + 20 = 0 dan 5x + 12y + 58 = 0
D. 12x + 5y − 20 = 0 dan 5x + 12y − 58 = 0
E. 12x + 5y − 20 = 0 dan 12x + 5y + 20 = 0
A. 5x + 12y − 20 = 0 dan 5x + 12y + 58 = 0
B. 5x + 12y + 20 = 0 dan 5x + 12y − 58 = 0
C. 5x + 12y + 20 = 0 dan 5x + 12y + 58 = 0
D. 12x + 5y − 20 = 0 dan 5x + 12y − 58 = 0
E. 12x + 5y − 20 = 0 dan 12x + 5y + 20 = 0
Pembahasan
Persamaan lingkaran pada soal di atas dapat disederhanakan dengan cara membagi 2 pada setiap sukunya.2x2 + 2y2 + 4x − 8y − 8 = 0
x2 + y2 + 2x − 4y − 4 = 0
Setelah itu, kita ubah bentuk umum tersebut menjadi bentuk baku dengan menggunakan kuadrat sempurna.
x2 + y2 + 2x − 4y = 4
(x + 1)2 + (y − 2)2 = 4 + 12 + (−2)2
(x + 1)2 + (y − 2)2 = 9
Bila dibandingkan dengan bentuk bakunya:
(x − x1)2 + (y − y1)2 = r2
Diperoleh:
x1 = −1
y1 = 2
r2 = 9
r = 3
Sementara itu, persamaan garis singgung lingkaran tersebut sejajar dengan garis 5x + 12y − 15 = 0. Artinya, gradien garis singgung lingkaran sama dengan gradien garis tersebut.
Gradien garis 5x + 12y − 15 = 0 adalah:
m = −a/b
= −5/12
Persamaan garis singgung lingkaran dengan gradien m dirumuskan:
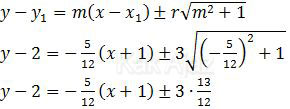
Kalikan semua suku dengan 12.
12y − 24 = −5(x + 1) ± 3∙13
12y − 24 = −5x −5 ± 39
Kita ambil nilai plus dan minus untuk persamaan di atas:
I. 12y − 24 = −5x −5 + 39
5x + 12y − 58 = 0
II. 12y − 24 = −5x −5 − 39
5x + 12y + 20 = 0
Jadi, persamaan garis singgung lingkaran tersebut adalah opsi (B).
Soal tentang Lingkaran UN 2012
Lingkaran L ∶ (x + 1)2 + (y − 3)2 = 9
memotong garis y = 3. Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah ….
A. x = 2 dan x = −4
B. x = 2 dan x = −2
C. x = −2 dan x = 4
D. x = −2 dan x = −4
E. x = 8 dan x = −10
memotong garis y = 3. Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah ….
A. x = 2 dan x = −4
B. x = 2 dan x = −2
C. x = −2 dan x = 4
D. x = −2 dan x = −4
E. x = 8 dan x = −10
Pembahasan
Titik potong antara lingkaran dan garis dapat dicari dengan cara substitusi y = 3 pada lingkaran L.(x + 1)2 + (y − 3)2 = 9
(x + 1)2 + (3 − 3)2 = 9
(x + 1)2 = 9
x + 1 = ±3
x = ±3 − 1
x1 = 2
x2 = −4
Sehingga titik potong lingkaran dan garis tersebut adalah:
(2, 3) dan (−4, 3)
Titik potong tersebut juga merupakan titik singgung lingkaran.
Persamaan garis singgung lingkaran (x + 1)2 + (y − 3)2 = 9 melalui (x1, y1) dirumuskan:
(x1 + 1)(x + 1) + (y1 − 3)(y − 3) = 9
Substitusi (2, 3) sebagai (x1, y1) diperoleh:
(2 + 1)(x + 1) + (3 − 3)(y − 3) = 9
3(x + 1) = 9
x + 1 = 3
x = 2
Substitusi (−4, 3) sebagai (x1, y1) diperoleh:
(−4 + 1)(x + 1) + (3 − 3)(y − 3) = 9
−3(x + 1) = 9
x + 1 = −3
x = −4
Jadi, garis singgung lingkaran tersebut adalah x = 2 dan x = −4 (A).
Pembahasan soal Lingkaran yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 9
Pembahasan Matematika IPA UN 2014 No. 9
Pembahasan Matematika IPA UN 2015 No. 9 dan 10
Pembahasan Matematika IPA UN 2016 No. 25
Pembahasan Matematika IPA UN 2017 No. 34 dan 35
Pembahasan Matematika IPA UN 2018 No. 27 dan 28
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

Aku mau berterima kasih bangett dgn bapak, karena akhirnya aku bisa mengerti persamaan garis lingkaran setelah sekian lama dan walaupun aku baca buku UN ku tetap aja aku nggak ngerti tapi aku sangat bersyukur karena blog bapak ini. Inshaa Allah yah pak pahala bapak mengalir terus menerus karena aku yakin banyak banget yang terbantu dgn blog bapak ini salah satunya aku. Terima kasih telah memudahkan, Inshaa Allah berkah yah buat bapak😊
ReplyDeleteAmin Ya Rabbal Alamin.
DeleteTerima kasih banyak Nabila, atas apresiasinya terhadap blog ini. Semoga lebih gemar matematika dan lebih semangat belajar.
Aamiin, terima kasih sdh menyemangatkan. Hari senin aku sdh UN dan bkn hanya pembahasan mtk UN saja yang aku buka, aku juga akan membuka pembahasan fisika UN karena Inshaa Allah aku mau ambil fisika. Dan alasan terbesar aku terus buka blog bapak karena Mashaa Allah banget karena aku lebih mudah memahami soal-soal. Sekali lagi Inshaa Allah berkah yah atas apa yang bapak kerjakan😊 Ini adalah salah satu amalan bapak yang akan terus menerus mengalir AAMIIN😊
ReplyDeleteAmin, terima kasih atas doa-doanya.
DeleteSemoga sukses menghadapi UN dan mendapatkan hasil yang optimal.
Aamiin terima kasih juga atas doanya😊
ReplyDeleteSettingan?
ReplyDelete?????
Delete