Pembahasan Matematika IPA UN 2013 No. 6 - 10

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 6 sampai dengan nomor 10 tentang:

• fungsi kuadrat, 
• persamaan kuadrat, 
• sistem persamaan linear, 
• persamaan lingkaran, dan 
• suku banyak.

Soal No. 6 tentang Fungsi Kuadrat

Fungsi f(x) = 2x² − ax + 2 akan menjadi fungsi definit positif bila nilai a berada pada interval ….

A.   a > −4
B.   a > 4
C.   −4 < a < 4
D.   4 < a < 6
E.   −6 < a  <4

Pembahasan

Dari fungsi f(x) = 2x² − ax + 2 diperoleh:

a = 2
b = −a
c = 2

Definit positif berarti berapa pun nilai x akan selalu menghasilkan f(x) positif. Syaratnya adalah:

• Grafik fungsinya terbuka ke atas.

a > 0
(sudah terpenuhi karena a = 2)

• Grafik fungsinya tidak memotong sumbu x.

                      D < 0
           b² − 4ac < 0
(−a)² − 4 ∙ 2 ∙ 2 < 0
             a² − 16 < 0
   (a + 4)(a − 4) < 0
       −4 < a < 4

Jadi, agar fungsi kuadrat tersebut definit positif maka interval nilai a adalah −4 < a < 4 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Fungsi Kuadrat

Soal No. 7 tentang Persamaan Kuadrat

Diketahui persamaan kuadrat mx² − (2m − 3)x + (m − 1) = 0. Nilai m yang menyebabkan akar-akar persamaan kuadrat tersebut real dan berbeda adalah ….

A.   m > 13/12, m ≠ 0
B.   m < 9/8, m ≠ 0
C.   m > 9/8, m ≠ 0
D.   m < 9/4, m ≠ 0
E.   m > 9/4, m ≠ 0

Pembahasan

Dari persamaan kuadrat mx² − (2m − 3)x + (m − 1) = 0 diperoleh:

a = m
b = −(2m - 3)
   = −2m + 3
c = m − 1

Agar mempunyai akar real dan berbeda maka persamaan kuadrat tersebut harus mempunyai diskriminan positif.

                                        D > 0
                              b² − 4ac > 0
     (−2m + 3)² − 4m(m − 1) > 0
4m² − 12m + 9 − 4m² + 4m > 0
                                     −8m > −9
                                       8m < 9 [tanda berubah]
                                         m < 9/8

Agar mempunyai dua akar (ciri persamaan kuadrat) maka:

a ≠ 0
m ≠ 0

Jadi, agar persamaan kuadrat tersebut mempunyai akar real dan berbeda maka nilai m yang memenuhi adalah m < 9/8, m ≠ 0 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Kuadrat

Soal No. 8 tentang Sistem Persamaan Linear

Lima tahun yang akan datang, jumlah umur kakak dan adik adalah 6 kali selisihnya. Sekarang, umur kakak 6 tahun lebih dari umur adik. Umur kakak sekarang adalah ….

A.   21 tahun
B.   16 tahun
C.   15 tahun
D.   10 tahun
E.   6 tahun

Pembahasan

Misal:

a : umur adik sekarang
k : umur kakak sekarang

Sekarang umur kakak 6 tahun lebih dari umur adik.

k = a + 6
a = k − 6 … (1)

Lima tahun yang akan datang, jumlah umur kakak dan adik adalah 6 kali selisihnya.

(k + 5) + (a + 5) = 6[(k + 5) - (a + 5)]
          k + a + 10 = 6(k − a)
          k + a + 10 = 6k − 6a
              7a + 10 = 5k            … (2)

Substitusi persamaan (1) ke persamaan (2), diperoleh:

7(k − 6) + 10 = 5k
7k − 42 + 10 = 5k
                 2k = 32
                   k = 16

Jadi, umur kakak sekarang adalah 16 tahun (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sistem Persamaan Linear

Soal No. 9 tentang Persamaan Lingkaran

Persamaan lingkaran yang berpusat di titik (4, −3) dan berdiameter 4√17 adalah ….

A.   x² + y² − 8x + 6y − 57 = 0
B.   x² + y² − 8x + 6y − 43 = 0
C.   x² + y² − 8x − 6y − 43 = 0
D.   x² + y² + 8x − 6y − 15 = 0
E.   x² + y² + 8x − 6y − 11 = 0

Pembahasan

Diketahui:

Pusat lingkaran (a, b) = (4, −3)
Jari-jari lingkaran r = ½ × 4√17
                                = 2√17

Persamaan lingkaran dengan pusat (a, b) dan jari-jari r adalah:

                    (x − a)² + (y − b)² = r²
                    (x − 4)² + (y + 3)² = (2√17)²
        x² − 8x + 16 + y² + 6y + 9 = 68
x² + y² − 8x + 6y + 16 + 9 − 68 = 0
               x² + y² − 8x + 6y − 43 = 0

Jadi, persamaan lingkaran tersebut adalah opsi (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran

Soal No. 10 tentang Suku Banyak

Diketahui salah satu faktor linear dari suku banyak f(x) = 2x⁴ − 3x² + (p − 15)x + 6 adalah (2x − 1). Faktor linear lainnya dari suku banyak tersebut adalah ….

A.   x − 5
B.   x − 2
C.   x + 1
D.   x + 2
E.   x + 3

Pembahasan

Cara sudah lumrah dalam menyelesaikan soal di atas adalah cara skematik atau Horner.

Suku banyak f(x) = 2x⁴ − 3x² + (p − 15)x + 6 habis dibagi (2x − 1).

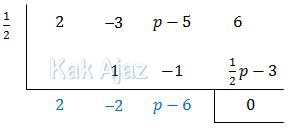
Dari kolom terakhir diperoleh:

6 + ½p − 3 = 0
             ½p = −3
                p = −6

Sehingga pada baris terakhir (tercetak biru) diperoleh:

2     −2     −12

Yang berarti:

2x² − 2x − 12 = 0
      x² − x − 6 = 0
(x − 3)(x + 2) = 0

Dengan demikian, faktor yang lain adalah:

(x − 3) atau (x + 2)

Jadi, sesuai opsi jawaban yang ada, faktor lain dari suku banyak tersebut adalah (x + 2) (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Suku Banyak

Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.