Pembahasan Matematika IPS UN 2017 No. 11 - 15

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 11 sampai dengan nomor 15 tentang:

• sistem pertidaksamaan linear, 
• model matematika program linear, 
• nilai optimum sistem pertidaksamaan, 
• nilai optimum program linear, dan 
• persamaan matriks.

Soal No. 11 tentang Sistem Pertidaksamaan Linear

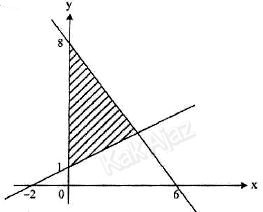
Daerah yang diarsir pada grafik di bawah ini merupakan penyelesaian dari sistem pertidaksamaan ….

A.   2x − y ≤ 2, 4x + 3y ≤ 24, x ≥ 0, y ≥ 0
B.   2y − x ≤ 2, 4x + 3y ≥ 24, x ≥ 0, y ≥ 0
C.   2y − x ≤ 2, 4x + 3y ≤ 24, x ≥ 0, y ≥ 0
D.   2y − x ≥ 2, 4x + 3y ≤ 24, x ≥ 0, y ≥ 0
E.   2x − y ≥ 2, 4x + 3y ≤ 24, x ≥ 0, y ≥ 0

Pembahasan

Misalkan garis (1) adalah garis yang melalui titik (−2, 0) dan (0, 1).

Angka 1 yang berada pada sumbu y kita kalikan dengan x. Sedangkan angka −2 yang berada pada sumbu x kita kalikan dengan y. Hasilnya adalah perkalian angka 1 dan −2.

Sehingga persamaan garis (1) adalah:

1x − 2y = 1×(−2)
  x − 2y = −2
  2y − x = 2

Karena daerah yang diarsir berada di atas garis (1) maka pertidaksamaannya menggunakan tanda ‘≥’. [saat menentukan tanda pertidaksamaan, variabel y harus positif]

2y − x ≥ 2

Sedangkan garis (2) adalah garis yang melalui titik (6, 0) dan (0, 8). Dengan cara yang sama, persamaan garis (2) adalah:

8x + 6y = 8×6
8x + 6y = 48
4x + 3y = 24

Karena yang diarsir berada di bawah/kiri garis (2) maka pertidaksamaannya menggunakan tanda ‘≤’.

4x + 3y ≤ 24

Pada grafik pertidaksamaan di atas, daerah yang diarsir berada di kuadran I (berada pada daerah x positif dan y positif).

x ≥ 0, y ≥ 0

Jadi, daerah yang diarsir pada grafik di atas adalah penyelesaian dari sistem pertidaksamaan pada opsi (D).

Soal No. 12 tentang Model Matematika Program Linear

Seorang peternak memiliki tidak lebih dari 8 kandang untuk memelihara kambing dan sapi. Setiap kandang dapat menampung kambing sebanyak 15 ekor atau menampung sapi sebanyak 6 ekor. Jumlah ternak yang direncanakan tidak lebih dari 100 ekor. Jika banyak kandang yang berisi kambing x buah dan yang berisi sapi y buah, model matematika untuk kegiatan peternak tersebut adalah ….

A.   8x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
B.   15x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
C.   6x + 15y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
D.   8x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
E.   15x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0

Pembahasan

Diketahui:

x : kandang kambing
y : kandang sapi

Perhatikan kalimat yang pertama!

Seorang peternak memiliki tidak lebih dari 8 kandang untuk memelihara kambing dan sapi.

Artinya, jumlah kandang kambing dan kandang sapi tidak lebih dari (kurang atau sama dengan) 8 kandang.

x + y ≤ 8

Sedangkan kalimat yang kedua dan ketiga berarti bahwa setiap kandang kambing berisi 15 ekor dan kandang sapi berisi 6 ekor. Jumlah kambing dalam kandang (15x) dan sapi dalam kandang (6y) tidak lebih dari 100 ekor.

15x + 6y ≤ 100

Karena jumlah kandang tidak mungkin negatif maka berlaku:

x ≥ 0, y ≥ 0

Jadi, model matematika untuk kegiatan peternak tersebut yang tepat adalah opsi (B).

Soal No. 13 tentang Nilai Optimum Sistem Pertidaksamaan

Diketahui sistem pertidaksamaan

5x + 2y ≤ 80, x + 4y ≥ 25, x ≥ 0, y ≥ 0

Nilai maksimum dari f(x, y) = 100x + 4y yang memenuhi pertidaksamaan tersebut adalah ….

A.   25
B.   160
C.   1510
D.   1600
E.   2500

Pembahasan

Untuk menyelesaikan soal di atas, seharusnya digambar terlebih dahulu grafik sistem pertidaksamaannya. Namun untuk soal UN, nilai maksimum atau minimumnya biasanya terletak pada titik potong kedua garis.

Titik potong kedua garis dapat dicari dengan mengeliminasi persamaan garisnya.

5x + 2y = 80 |×2| 10x + 4y = 160
  x + 4y = 25 |×1|     x + 4y = 25
                           ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
                                      9x = 135
                                        x = 15

Selanjutnya, x = 15 kita substitusikan ke salah satu persamaan garis, misal garis kedua.

  x + 4y = 25
15 + 4y = 25
        4y = 10
          y = 5/2

Dengan demikian, nilai maksimum fungsi f(x, y) terletak pada titik (15, 5/2).

     f(x, y) = 100x + 4y
f(15, 5/2) = 100×15 + 4×5/2
                = 1500 + 10
                = 1510

Jadi, nilai maksimum dari fungsi f(x, y) adalah 1510 (C).

Soal No. 14 tentang Nila Optimum Program Linear

Sebuah toko kain menyediakan dua jenis kain batik yaitu batik halus dan batik cap. Etalase kain batik toko tersebut dapat menampung maksimum sebanyak 36 kain batik. Harga satuan kain batik halus Rp800.000,00 dan harga satuan kain batik cap Rp600.000,00. Modal yang disediakan untuk penyediaan kain batik tidak lebih dari Rp24.000.000,00. Keuntungan penjualan adalah Rp120.000 per kain batik halus dan Rp100.000,00 per kain batik cap. Banyak kain batik yang harus disediakan agar diperoleh keuntungan maksimum dari penjualan semua kain batik tersebut adalah ….

A.   36 kain batik halus saja
B.   36 kain batik halus dan 30 kain batik cap
C.   30 kain batik halus dan 36 kain batik cap
D.   24 kain batik halus dan 12 kain batik cap
E.   12 kain batik halus dan 24 kain batik cap

Pembahasan

Cara yang efektif menyelesaikan soal program linear adalah dengan memanfaatkan tabel bantuan sebagai berikut:

	Batik halus (x)	Batik cap (y)	36
Harga beli	800.000 4	600.000 3	24.000.000 120
Keuntungan	120.000	100.000

Keterangan: angka yang dicoret berarti masing-masing dibagi 200.000.

Berdasarkan tabel bantuan di atas diperoleh persamaan:

    x + y = 36   |×4|  4x + 4y = 144
4x + 3y = 120 |×1|  4x + 3y = 120
                              ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
                                         y = 24

Substitusi y = 24 ke persamaan yang pertama diperoleh:

  x + y = 36
x + 24 = 36
        x = 12

Jadi, agar diperoleh keuntungan maksimum maka kain batik halus yang terjual adalah 12 sedangkan kain batik cap harus terjual 24 (E).

Soal No. 15 tentang Persamaan Matriks

Ibu Giat dan Ibu Prestasi berbelanja di toko Bahagia. Ibu Giat membeli 2 kg gula dan 3 kg beras, dan ia harus membayar Rp64.000,00. Sedangkan Ibu Prestasi membeli 5 kg gula dan 4 kg beras, dan ia harus membayar Rp118.000,00. Toko Bahagia menjual gula dengan harga x rupiah tiap kilo dan beras dengan harga y rupiah tiap kilo. Permasalahan tersebut dapat ditampilkan dalam bentuk persamaan matriks ….

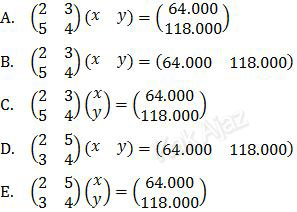
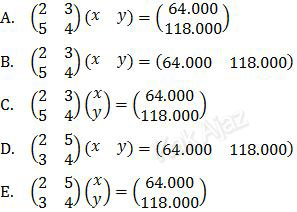
Pembahasan

Diketahui:

x : harga 1 kg gula
y : harga 1 kg beras

Persamaan dalam x dan y pada permasalahan di atas adalah:

Ibu Giat      : 2x + 3y = 64.000
Ibu Prestasi : 5x + 4y = 118.000

Jika persamaan di atas diubah dalam bentuk matriks maka:

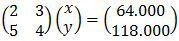
Jadi, tampilan persamaan matriks yang tepat pada permasalahan di atas adalah opsi (C).

Simak Pembahasan Soal Matematika IPS UN 2017 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.