Pembahasan Matematika IPA UN: Logaritma

Spiral Logaritma

Pembahasan soal-soal Ujian Nasional SMA-IPA bidang studi Matematika dengan materi pembahasan Logaritma.

Soal tentang Logaritma UN 2014

Hasil dari

$Logaritma UN 2014$

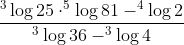
adalah ....

A.   11/4
B.   15/4
C.   17/4
D.   11
E.   15

Pembahasan

Angka-angka yang perlu disesuaikan

25 = 5²
81 = 3⁴
36 = 2².3²
4   = 2²

Rumus-rumus yang dibutuhkan untuk mengerjakan soal di atas.

^alog a            = 1
log ab            = log a + log b
^alog bⁿ           = n ^alog b
^aⁿlog b           = 1/n ^alog b
^alog b ^blog c = ^alog c

Dengan rumus-rumus tersebut, mari kita kerjakan soal di atas.

$\frac{^{3}\log 25\cdot ^{5}\log 81-^{4}\log 2}{^{3}\log 6- ^{3}\log 4}=\frac{^{3}\log 5^{2}\cdot ^{5}\log 3^{4}-^{2^{2}}\log 2}{^{3}\log 2^{2}\cdot 3^{2}- ^{3}\log 2^{2}}$
$=\frac{2\cdot 4\; ^{3}\log 5\cdot ^{5}\log 3-\frac{1}{2}^{2}\log 2}{2\; ^{3}\log 2+2\; ^{3}\log 3- 2\; ^{3}\log 2}$
$=\frac{8-\frac{1}{2}}{2}$
$=\frac{15/2}{2}$
= 15/4

Jadi, hasil dari logaritma tersebut adalah 15/4 (B).

Soal tentang Logaritma UN 2015

Hasil dari

$Soal logaritma UN 2015$

adalah ....

A.   45/4
B.   5/9
C.   1/3
D.   −1/3
E.   −5/9

Pembahasan

Angka-angka yang perlu disesuaikan

√5   = 5^1/2
³√5 = 5^1/3
1/3 = 3⁻¹
1/5   = 5⁻¹
1/27 = 3⁻³
3√3 = 3¹. 3^1/2
        = 3^3/2

Dengan menggunakan rumus-rumus di atas, mari kita kerjakan soal tersebut dengan perlahan-lahan.

$\frac{^{3}\log \sqrt{5}\cdot ^{\sqrt[3]{5}}\log\frac{1}{3}+^{5}\log\frac{1}{5}}{^{3}\log\frac{1}{27}-^{3}\log3\sqrt{3}}=\frac{^{3}\log 5^{\frac{1}{2}}\cdot ^{5^{\frac{1}{3}}}\log3^{-1}+^{5}\log5^{-1}}{^{3}\log3^{-3}-^{3}\log3^{\frac{3}{2}}}$
                                    $=\frac{\frac{1}{2}\cdot 3\cdot (-1)+(-1)}{-3-\frac{3}{2}}$
                                    $=\frac{-5/2}{-9/2}$
                                    = 5/9

Jadi, hasil dari logaritma tersebut adalah 5/9 (B).

Soal tentang Logaritma UN 2010

Hasil dari

^1/5log 625 + ⁶⁴log (1/16) + 4^{3²⁵log 5}

aadalah ....

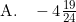
$\textrm{A. }\; \; -4\frac{19}{24}$
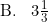
$\textrm{B. }\; \; 3\frac{1}{3}$
$\textrm{C. }\; \; 4\frac{2}{3}$
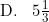
$\textrm{D. }\; \; 5\frac{1}{3}$
$\textrm{E. }\; \; 59\frac{1}{3}$

Pembahasan

Kita kerjakan per suku saja supaya lebih santai.

^1/5log 625 = ^5⁻¹log 5⁴
                = −4 ⁵log 5
                = −4

⁶⁴log (1/16) = ^2⁶log 2⁻⁴
                   = −4/6
                   = −2/3

4^{3²⁵log 5} = 4^{3^5²log 5}
             = 4^{3.½ ⁵log 5}
             = 4^3/2
             = (2^2)3/2
             = 2³
             = 8

Dengan demikian,

^1/5log 625 + ⁶⁴log (1/16) + 4^{3²⁵log 5}
= −4 − 2/3 + 8
= 4 − 2/3
= 10/3
= 3⅓

Jadi, hasil dari logaritma tersebut adalah opsi (B).

Soal tentang Logaritma UN 2012

Diketahui ²log 3 = x dan ²log 10 = y. Nilai ⁶log 120 = ....

$\textrm{A. }\; \; \frac{x+y+2}{x+1}$
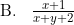
$\textrm{B. }\; \; \frac{x+1}{x+y+2}$
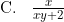
$\textrm{C. }\; \; \frac{x}{xy+2}$
$\textrm{D. }\; \; \frac{xy+2}{x}$
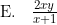
$\textrm{E. }\; \; \frac{2xy}{x+1}$

Pembahasan

Angka 6 kita ubah menjadi 2×3 sedangkan angka 120 kita ubah menjadi 2²×3×10. Sebelumnya kita gunakan rumus

$^{a}\log b=\frac{\log b}{\log a}$

Dengan demikian diperoleh:

$^{6}\log 120=\frac{\log 120}{\log 6}$

Agar bentuk dapat diselesaikan, kita ubah bilangan pokoknya menjadi 2 (bilangan pokok boleh diganti berapapun, asal sama).

⁶log 20
$=\frac{^{2}\log 120}{^{2}\log 6}$
$=\frac{^{2}\log 2^{2}\cdot 3\cdot 10}{^{2}\log 2\cdot 3}$
$=\frac{2\; ^{2}\log 2+ ^{2}\log3+^{2}\log 10}{^{2}\log 2+^{2}\log 3}$
$=\frac{2+x+y}{1+x}$

Jadi, nilai dari ⁶log 120 adalah opsi (A).

Soal tentang Logaritma UN 2013

Diketahui ²log 3 = a dan ²log 5 = b. Nilai dari ⁹log 150 dalam a dan b adalah ….

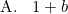
$\textrm{A. }\; \; 1+b$
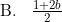
$\textrm{B. }\; \; \frac{1+2b}{2}$
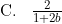
$\textrm{C. }\; \; \frac{2}{1+2b}$
$\textrm{D. }\; \; \frac{1+a+2b}{2a}$
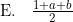
$\textrm{E. }\; \; \frac{1+a+b}{2}$

Pembahasan

Untuk menyelesaikan soal ini, angka 9 dan 150 harus kita uraikan sedemikian hingga mencakup angka 2, 3, atau 5 yang diketahui pada soal.

⁹log 150 = ^3²log 2 . 3 . 5²
              = ½ ³log 2 . 3 . 5²
              = ½ (³log 2 + ³log 3 + ³log 5²)
              = ½ (1/a + 1 + 2 ³log 5)

Biarkan sebentar, kita kerjakan dulu ³log 5.

$^{3}\log 5=\frac{\log 5}{\log3}$
            $=\frac{^{2}\log 5}{^{2}\log3}$
             = b/a

Sekarang mari kita lanjutkan

⁹log 150 = ½ (1/a + 1 + 2 ³log 5)
              = ½ (1/a + 1 + 2b/a)
              $=\frac{1}{2a}+\frac{1}{2}+\frac{b}{a}$
              $=\frac{1+a+2b}{2a}$

Jadi, nilai dari ⁹log 150 adalah opsi (D).

Pembahasan soal Logaritma yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 4
Pembahasan Matematika IPA UN 2014 No. 5
Pembahasan Matematika IPA UN 2015 No. 5
Pembahasan Matematika IPA UN 2016 No. 3
Pembahasan Matematika IPA UN 2017 No. 1
Pembahasan Matematika IPA UN 2018 No. 1

Simak juga:
Pembahasan Matematika IPA UN: Pertidaksamaan Eksponen dan Logaritma
Pembahasan Matematika IPA UN: Perpangkatan
Pembahasan Matematika IPA UN: Bnetuk Akar

Dapatkan pembahasan soal dalam file pdf di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

10 comments:

Unknown16 December 2017 at 16:38
Cara menghitung ini bagaimana 1/2×3(-1)+(-1)=
(UN 2015)
Unknown17 December 2017 at 11:18
Terimakasih atas penjelasannya
Unknown2 April 2018 at 20:41
Penyelesaian ini gi mana ya
3log49.7log27+2log1/8-2log32
Mohon bantuannya
Terimakasih
Unknown31 October 2018 at 20:30
Cara ngitung ini gimana? 6log (Xpangkat 2 - 4x - 50) -6log(2x+6) = 2log3/log6
Unknown3 July 2019 at 07:10
Jika 7^log2^log3^log x = 0, maka x =...
Mohon bantuannya kak Ajaz.
Terima kasih sebelumnya

Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.

Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan

Wednesday, 24 February 2016