Pola Bilangan

Pola bilangan adalah urutan bilangan yang mengikuti pola tertentu. Pola bilangan tersebut bisa berbentuk lambang bilangan atau berbentuk geometris.

Tokoh Pola Bilangan

Blaise Pascal adalah seorang ilmuwan Prancis yang lahir pada tanggal 19 Juni 1623. Meski tidak pernah menempuh pendidikan secara resmi di sekolah, ia dikenal sebagai anak yang cerdas. Semua ilmu pengetahuan diajarkan langsung oleh ayahnya.

Blaise Pascal (1623 - 1662)

Pada usia 12 tahun, ia menemukan rumus-rumus dasar geometri dan menemukan mesin hitung. Di usianya yang masih 14 tahun, ia aktif mengikuti pertemuan mingguan kelompok matematikawan Prancis.

Selain mendalami matematika, ia juga mendalami ilmu alam. Hukum Pascal yang berlaku pada benda cair adalah hasil pengkajiannya.

Pola bilangan segitiga Pascal yang terkenal itu, ia temukan ketika berusia 30 tahun. Pola bilangan ini ternyata mencakup hampir semua pola bilangan yang ada. Berpegang pada pola bilangan ini pula, ia mengembangkan teori probabilitas.

Sayangnya, usia Pascal tidak panjang. Ia meninggal di usia yang relatif muda, 39 tahun.

Pola Bilangan Ganjil

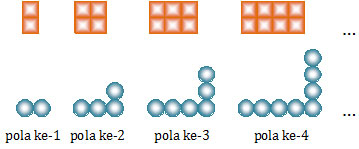
Pola bilangan ganjil adalah pola bilangan asli yang bernilai ganjil dan terurut dari bilangan terkecil.

Selisih antarpola

Jika diperhatikan gambar di atas, pola bilangan ganjil terbentuk dengan menambahkan 1 bola di atas dan 1 bola di sebelah kiri dari pola sebelumnya. Dengan mengetahui pola ini maka pola berikutnya dapat ditentukan dengan mudah.

Jumlah bola yang tersusun pada pola berikutnya merupakan penambahan 2 bola dari pola sebelumnya.

Pola ke-n

Untuk menentukan pola ke-60, misalnya, tidak mungkin kita mengurutkan pola tersebut sampai 60 pola.

Perhatikan ilustrasi berikut ini!

Berdasarkan ilustrasi di atas kita peroleh

• Pola ke-1 : 1 + 0 = 1
• Pola ke-2 : 2 + 1 = 3
• Pola ke-3 : 3 + 2 = 5
• Pola ke-4 : 4 + 3 = 7
• Pola ke-n : n + (n − 1) = 2n − 1

Pola ke-n pada pola bilangan ganjil adalah 2n − 1

Jumlah n Pola Pertama

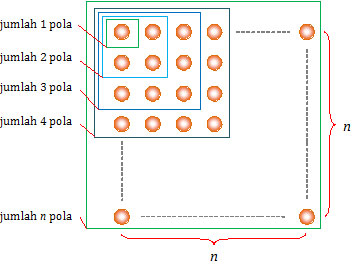
Jika jumlah bola pada pola ke-1, ke-2, ke-3, dan seterusnya dijumlahkan maka akan didapatkan gambaran sebagai berikut.

Berdasarkan ilustrasi di atas diperoleh:

• Jumlah 1 pola pertama = 1 × 1 = 1
• Jumlah 2 pola pertama = 2 × 2 = 4
• Jumlah 3 pola pertama = 3 × 3 = 9
• Jumlah 4 pola pertama = 4 × 4 = 16
• Jumlah n pola pertama = n × n = n²

Jadi 1 + 3 + 5 + 7 + 9 + … + (2n − 1) = n²

Jumlah n pola pertama pada pola bilangan ganjil adalah n²

Pola Bilangan Genap

Pola bilangan genap adalah pola bilangan yang tersusun dari bilangan genap dan terurut dari bilangan genap terkecil. Bilangan genap yang dimaksud dalam pola ini adalah bilangan genap yang merupakan bilangan asli. Jadi, bilangan nol dan negatif tidak termasuk dalam pola ini.

Selisih antarpola

Pola berikutnya pada pola bilangan genap sama halnya dengan pola bilangan ganjil, yaitu berbeda 2 dari pola sebelumnya.

Pola ke-n

Perhatikan ilustrasi berikut ini!

Berdasarkan ilustrasi di atas kita peroleh

• Pola ke-1 : 1 + 1 = 2
• Pola ke-2 : 2 + 2 = 4
• Pola ke-3 : 3 + 3 = 6
• Pola ke-n : n + n = 2n

Pola ke-n pada pola bilangan genap adalah 2n

Pola ke-n juga dapat dicari dengan cara berikut

• Pola ke-1 : 2 × 1 = 2
• Pola ke-2 : 2 × 2 = 4
• Pola ke-3 : 2 × 3 = 6
• Pola ke-n : 2 × n = 2n

Jumlah n Pola Pertama

Perhatikan ilustrasi berikut ini!

Jumlah n pola pertama dapat ditentukan dengan cara berikut:

• Jumlah 1 pola pertama = 1 × 2 = 2
• Jumlah 2 pola pertama = 2 × 3 = 6
• Jumlah 3 pola pertama = 3 × 4 = 12
• Jumlah 4 pola pertama = 4 × 5 = 20
• Jumlah n pola pertama = n × (n+1) = n² + n

Jadi, 2 + 4 + 6 + 8 + 10 + … + 2n = n² + n

Jumlah n pola pertama pada pola bilangan genap adalah n(n + 1) atau n² + n

Pola Bilangan Persegi

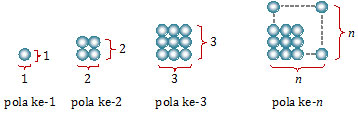
Pola bilangan persegi adalah pola bilangan yang geometrinya membentuk bangun persegi.

Pola ke-n

Berdasarkan gambar di atas diperoleh

• Pola ke-1 : 1 × 1 = 1
• Pola ke-2 : 2 × 2 = 4
• Pola ke-3 : 3 × 3 = 9
• Pola ke-n : n × n = n²

Pola ke-n pada pola persegi adalah n²

Selisih antarpola

Pola bilangan persegi mempunyai selisih antarpola yang selalu berubah. Tetapi perubahan selisih tersebut juga berpola. Perhatikan ilustrasi berikut!

Pola Bilangan Segitiga

Pola bilangan segitiga adalah pola bilangan yang geometri membentuk bangun segitiga.

Pada gambar di atas, pola bilangan segitiga ditunjukkan oleh bola yang berwarna orange, sedangkan bola yang berwarna putih hanya sebagai bola pertolongan untuk memudahkan menentukan pola ke-n.

Pola ke-n

Dengan menggunakan bola-bola penolong yang berwarna putih, secara keseluruhan membentuk pola persegi panjang. Sedangkan pola segitiga merupakan setengah dari pola persegi panjang.

Berdasarkan gambar di atas diperoleh

• Pola ke-1 : ½ × 1 × 2 = 1
• Pola ke-2 : ½ × 2 × 3 = 3
• Pola ke-3 : ½ × 3 × 4 = 6
• Pola ke-n : ½ × n × (n + 1) = ½ n(n + 1)

Pola ke-n pada pola segitiga adalah ½ n(n + 1)

Pola Bilangan Fibonacci

Pola bilangan ini pertama kali dijelaskan oleh matematikawan India, Gopala dan Hemachandra pada tahun 1150. Oleh kedua matematikawan tersebut, pola bilangan ini digunakan untuk menyelidiki berbagai kemungkinan memasukkan barang-barang ke dalam kantong.

Di dunia barat, pola bilangan ini dipelajari oleh Leonardo da Pisa atau dikenal dengan nama Fibonacci sekitar tahun 1200. Fibonacci mempelajari pola bilangan ini ketika mengamati pertumbuhan ideal populasi kelinci. Sekarang, pola bilangan ini lebih dikenal dengan sebut pola bilangan Fibonacci.

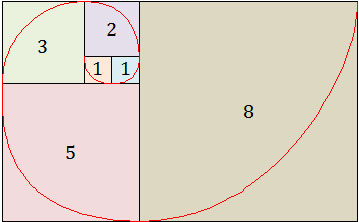
Pola bilangan Fibonacci diawali dengan bilangan 1, pola kedua juga 1. Sedangkan pola ketiga dan seterusnya merupakan jumlah dari dua pola sebelumnya.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, …

Mulai pola ke-13, yaitu 233, bila dibandingkan dengan pola sebelumnya akan menghasilkan nilai yang sama.

233 : 144 = 1,618
377 : 233 = 1,618
610 : 377 = 1,618
987 : 610 = 1,618
dan seterusnya

Pola Bilangan Segitiga Pascal

Sesuai namanya, pola bilangan ini ditemukan oleh Blaise Pascal, matematikawan Prancis, meskipun berabad-abad sebelumnya pola ini sudah dikaji oleh matematikawan India, Persia, Cina, dan Italia.

Pola bilangan segitiga Pascal diawali dengan bilangan 1 pada puncak segitiga. Kemudian di bawahnya, di tepi kiri dan kanan segitiga juga ditulis bilangan 1. Selanjutnya, setiap kali mengawali dan mengakhiri barisan selalu ditulis bilangan 1. Sedangkan bilangan-bilangan di antara tepi kiri dan kanan merupakan penjumlahan dari dua bilangan di atasnya.

Untuk lebih jelasnya perhatikan gambar ilustrasi berikut ini!

Fakta tentang Pola Bilangan Segitiga Pascal

Perhatikan baik-baik pola bilangan segitiga Pascal berikut ini!

Jika diperhatikan dengan saksama maka dap[at diperoleh:

• Menunjukkan sifat komutatif penjumlahan

5 = 1 + 4 atau 5 = 4 + 1

• Diagonal berwarna hijau merupakan pola bilangan asli.

1, 2, 3, 4, 5, …, n

• Diagonal berwarna biru merupakan pola bila segitiga.

1, 3, 6, 10, …, ½ n(n + 1)

• Diagonal berwarna orange merupakan pola bilangan limas segitiga

1, 4, 10, …

• Jumlah bilangan setiap baris merupakan pola bilangan dengan rasio 2.

1, 2, 4, 8, 16, 32, …, 2ⁿ⁻¹

• Jumlah bilangan setiap diagonal merupakan pola bilangan Fibonacci.

1, 1, 2, 3, 5, 8, …

Aplikasi Pola Bilangan Segitiga Pascal

Penerapan pola bilangan segitiga dalam kehidupan sehari-hari di antaranya adalah

• Koefisien dari penjabaran pangkat binomial (a + b)ⁿ

(a + b)¹ = a + b                                 (1 : 1)
(a + b)² = a² + 2ab + b²                  (1 : 2 : 1)
(a + b)³ = a³ + 3a²b + 3ab² + b³    (1:3:3:1)
dan seterusnya sampai (a + b)ⁿ

• Rasio genotip persilangan monohibrid dominan dan intermediet

1 : 2 : 1

• Rasio fenotip persilangan monohibrid intermediet

1 : 2 : 1

• Rasio fenotip persilangan dihibrid dominan

1 : 3 : 3 : 1

• Probabilitas suatu kejadian

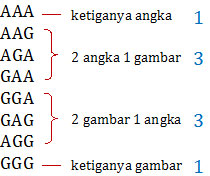
Jika 3 uang logam dilempar bersama maka semua kemungkinan muncul angka (A) dan gambar (G) adalah sebagai berikut:

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.