Pembahasan Matematika IPA UN: Limit Fungsi

Pembahasan soal-soal Ujian Nasional SMA-IPA bidang studi Matematika dengan materi pembahasan Limit Fungsi Aljabar dan Trigonometri.

Soal Limit Fungsi Aljabar UN 2011

Nilai dari



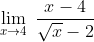
adalah ...

A.   0
B.   4
C.   8
D.   12
E.   16

Pembahasan

Limit fungsi aljabar di atas dapat diselesaikan dengan memanfaatkan rumus: 

a² − b² = (a − b)(a + b)

Dengan memahami bahwa x − 4 = (√x)² − 2², diperoleh:


                        
                          = √4 + 2
                          = 2 + 2
                          = 4

Jadi, nilai dari limit tersebut adalah 4 (B).

Soal Limit Fungsi Aljabar UN 2014

Nilai dari



adalah ....

A.   −3
B.   −2
C.   −1
D.   1
E.   3

Pembahasan

Bentuk umum dari limit fungsi aljabar tersebut adalah



Mari kita ubah limit tersebut ke bentuk umumnya.





Berdasarkan bentuk yang terakhir diperoleh: 

a = 25 
b = 10 
d = 20

Penyelesaian akhir limit tersebut adalah


        = −10/10
        = −1

Jadi, nilai dari limit fungsi aljabar tersebut adalah −1 (C).

Soal Limit Fungsi Trigonometri UN 2015

Nilai dari



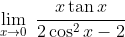
adalah ....

A.   −1/2
B.   −1/4
C.   0
D.   1/2
E.   1

Pembahasan

Prinsip limit fungsi trigonometri dengan nilai x mendekati nol adalah:

sin x = tan x = x

Dengan memahami prinsip tersebut, trigonometri bentuk cos x harus diupayakan sedemikian hingga menjadi bentuk sin x.



Bentuk cos pada penyebut harus diubah menjadi:

sin² x + cos² x = 1
       cos² x − 1 = −sin² x

Sehingga tahap penyelesaian limit tersebut menjadi:

   

Nah, sekarang tinggal mengganti tan x = x dan sin x = x  sehingga diperoleh:


= −1/2

Jadi, nilai dari limit fungsi trigonometri tersebut adalah −1/2 (A).

Soal Limit Fungsi Trigonometri UN 2014 (1)

Nilai dari



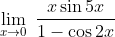
adalah ....

A.   0
B.   1/2
C.   1
D.   3/2
E.   5/2

Pembahasan

Yang harus diubah terlebih dahulu adalah bentuk (1 − cos 2x) dengan menggunakan rumus:

cos 2x = 1 − 2 sin² x
2 sin² x = 1 − cos 2x

Sehingga diperoleh:



Gantilah sin 5x = 5x dan sin² x = x² sehingga diperoleh:


= 5/2

Jadi, nilai dari limit fungsi trigonometri di atas adalah 5/2 (E).

Soal Limit Fungsi Trigonometri UN 2013

Nilai dari



adalah ....

A.   −4
B.   −3
C.   0
D.   4
E.   ∞

Pembahasan

Kita ubah dulu bentuk (x² − 4) menjadi (x − 2)(x + 2) sehingga diperoleh:



= lim_x→−2 (x − 2)
= −2 − 2
= −4

Jadi, nilai dari limit fungsi trigonometri tersebut adalah −4 (A).

Soal Limit Fungsi Trigonometri UN 2014 (2)

Nilai dari



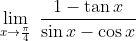
adalah ....

A.   −2√2
B.   −√2
C.   ½√2
D.   √2
E.   2√2

Pembahasan

Limit fungsi trigonometri seperti di atas lebih praktis dikerjakan dengan menurunkan pembilang dan penyebutnya. Rumus yang harus diingat tentang turunan fungsi trigonometri adalah sebagai berikut. 

y = sin x      y' = cos x
y = cos x     y' = −sin x
y = tan x     y' = sec² x
                      = 1/cos² x

Dengan memanfaatkan rumus turunan fungsi trigonometri tersebut diperoleh:



Ingat, cos 45° = ½√2 sehingga sec 45° = √2. Diperoleh:



=  −√2

Jadi, nilai limit fungsi trigonometri tersebut adalah −√2 (B).

Pembahasan soal limit fungsi yang lain bisa dilihat di:
Pembahasan Matematika IPA UN 2013 No. 28 dan 29
Pembahasan Matematika IPA UN 2014 No. 27 dan 28.
Pembahasan Matematika IPA UN 2015 No. 29 dan 30.
Pembahasan Matematika IPA UN 2016 No. 26 dan 27
Pembahasan Matematika IPA UN 2017 No. 19 dan 20
Pembahasan Matematika IPA UN 2018 No. 15
Pembahasan Matematika IPA UN 2018 No. 38 [isian]
Pembahasan Matematika IPA UN 2019 No. 14 dan 15
Pembahasan Matematika IPA UN 2019 (2) No. 15
Pembahasan Matematika PA UN 2019 (2) No. 16

Simak juga, Pembahasan Matematika IPA UN: Turunan Fungsi

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.