
Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 26 sampai dengan nomor 30 tentang:
- persamaan trigonometri,
- rumus jumlah dan selisih sinus dan kosinus,
- limit fungsi aljabar,
- limit fungsi trigonometri, serta
- aplikasi turunan.
Soal No. 26 tentang Persamaan Trigonometri
Nilai x memenuhi persamaan cos 2x − sin x = 0 untuk 0° < x < 360° adalah ….
A. {30°, 150°}
B. {30°, 270°}
C. {30°, 150°, 180°}
D. {60°, 120°, 300°}
E. {30°, 150°, 270°}
A. {30°, 150°}
B. {30°, 270°}
C. {30°, 150°, 180°}
D. {60°, 120°, 300°}
E. {30°, 150°, 270°}
Pembahasan
Langkah pertama adalah mengubah cos 2x. Rumus cos 2x ada tiga:- cos 2x = cos2x − sin2x
- cos 2x = 2cos2x − 1
- cos 2x = 1 − 2sin2x
Ok, mari kita selesaikan soal di atas!
cos 2x − sin x = 0
1 − 2sin2x − sin x = 0
2sin2x + sin x − 1 = 0
(2 sin x − 1)(sin x + 1) = 0
sin x = 1/2 atau sin x = −1
Untuk sin x = 1/2 berada di kuadran I dan II (positif)
- Kuadran I : sin x = sin 30°
x = 30°
- Kuadran II : sin x = sin(180° − 30°)
x = 150°Untuk sin x = −1 hanya ada satu nilai
sin x = sin 270°
x = 270°
Jadi, nilai x yang memenuhi persamaan trigonometri di atas adalah {30°, 150°, 270°} (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Trigonometri
Soal No. 27 tentang Rumus Jumlah dan Selisih Sinus dan Kosinus
Nilai dari
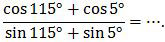
A. −√3
B. −1
C. −⅓√3
D. ⅓√3
E. √3
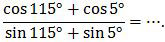
A. −√3
B. −1
C. −⅓√3
D. ⅓√3
E. √3

Pembahasan
Untuk menyelesaikan soal di atas, kita harus mengingat kembali dua rumus berikut ini:cos A + cos B = 2cos ½(A + B) cos ½(A − B)
sin A + sin B = 2sin ½(A + B) cos ½(A − B)〗
Berdasarkan rumus di atas maka:

Jadi, nilai dari bentuk trigonometri di atas adalah ⅓√3 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Perbandingan Trigonometri
Soal No. 28 tentang Limit Fungsi Aljabar
Nilai dari
limx→∞ [(2x − 1) − √(4x2 − 6x − 5)] = ⋯.
A. 4
B. 2
C. 1
D. 1/2
E. 1/4
limx→∞ [(2x − 1) − √(4x2 − 6x − 5)] = ⋯.
A. 4
B. 2
C. 1
D. 1/2
E. 1/4
Pembahasan
Bentuk limit di atas adalah: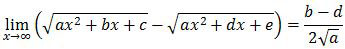
Itu artinya, kita harus mengubah bentuk limit pada soal menjadi bentuk seperti di atas. Yang kita ubah adalah 2x − 1.
2x − 1 = √[(2x − 1)2)
= √(4x2 − 4x + 1)
Dengan demikian,
limx→∞ [(2x − 1) − √(4x2 − 6x − 5)]
= limx→∞ [√(4x2 − 4x + 1) − √(4x2 − 6x − 5)]
Diperoleh:
a = 4
b = −4
d = −6
Sehingga hasilnya adalah:
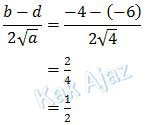
Jadi, nilai dari limit fungsi aljabar di atas adalah 1/2 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi
Soal No. 29 tentang Limit Fungsi Trigonometri
Nilai dari

A. −4
B. −3
C. 0
D. 4
E. ∞

A. −4
B. −3
C. 0
D. 4
E. ∞
Pembahasan
Limit trigonometri x → 0 berlaku:sin x = tan x = x
Limit pada soal di atas adalah limit trigonometri x → −2 atau sama dengan x + 2 → 0 sehingga berlalu:
sin(x + 2) = tan(x + 2) = x + 2 = p
Kak Ajaz misalkan saja sama dengan p supaya lebih mudah memahami saat mengerjakan nanti. Ok, kita selesaikan sekarang.

Jadi, nilai dari limit fungsi trigonometri di atas adalah −4 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi
Soal No. 30 tentang Aplikasi Turunan
Sebuah taman berbentuk persegi dengan keliling (2x + 24) m dan lebar (8 − x) m. Agar luas taman maksimum maka panjang taman tersebut adalah ….
A. 4 m
B. 8 m
C. 10 m
D. 12 m
E. 13 m
A. 4 m
B. 8 m
C. 10 m
D. 12 m
E. 13 m
Pembahasan
Sebuah taman berbentuk persegi panjang dengan keliling (2x + 24) m.K = 2x + 24
2(p + l) = 2x + 24
p + l = x + 12
Lebar taman adalah (8 − x) m. Kita substitusikan lebar taman ini pada persamaan di atas. Diperoleh:
p + 8 − x = x +12
p = 2x + 4
Luas taman tersebut adalah:
L = p × l
= (2x + 4)(8 − x)
= 16x − 2x2 + 32 − 4x
= −2x2 + 12x + 32
Agar luas taman maksimum maka turunan fungsi luas harus sama dengan nol.
L' = 0
−4x + 12 = 0
4x = 12
x = 3
Dengan demikian, panjang taman adalah:
p = 2x + 4
= 2 ∙ 3 + 4
= 10
Jadi, panjang taman tersebut adalah 10 m (C).
Perdalam materi ini di Pembahasan Matematika IPA UN: Titik Stasioner dan Nilai Ekstrem [Aplikasi Turunan]
Simak Pembahasan Soal Matematika IPA UN 2013 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan