- program linear,
- fungsi kuadrat,
- sistem persamaan linear,
- matriks, dan
- peluang kejadian.
Soal No. 1 tentang Program Linear
Seorang penjahit akan membuat 2 model pakaian. Dia mempunyai persediaan kain batik 40 meter dan kain polos 15 meter. Model A memerlukan 1 meter kain batik dan 1,5 meter kain polo, sedang model B memerlukan 2 meter kain batik dan 0,5 meter kain polos. Maksimum banyak pakaian yang mungkin dapat dibuat adalah ….
A. 10
B. 20
C. 22
D. 25
E. 30
A. 10
B. 20
C. 22
D. 25
E. 30
Pembahasan
Kita buat dulu tabel bantuan untuk soal di atas agar lebih mudah dipahami.| Model A (x) | Model B (y) | ? | |
| Kain batik | 1 | 2 | 40 |
| Kain polos | 1,5 | 0,5 | 15 |
Berdasarkan tabel bantuan di atas dapat dibuat model matematika sebagai berikut:
x + 2y = 40 |×2| 2x + 4y = 80
1,5x + 0,5 y = 15 |×2| 3x + y = 30
—————— +
5x + 5y = 110
x + y = 22 [kedua ruas dibagi 5]
Jadi, maksimum banyak pakaian yang mungkin dapat dibuat adalah 22 pakaian (C).
Soal No. 2 tentang Fungsi Kuadrat
Untuk 0 < a < 10, fungsi kuadrat f(x) = ax2 + 2ax + 10 memenuhi sifat ….
A. selalu negatif
B. selalu positif
C. hanya positif di setiap x, dengan 0 < x < 10
D. hanya negatif di setiap x, dengan 0 < x < 10
E. hanya positif di setiap x, dengan x < 0 atau x > 10
A. selalu negatif
B. selalu positif
C. hanya positif di setiap x, dengan 0 < x < 10
D. hanya negatif di setiap x, dengan 0 < x < 10
E. hanya positif di setiap x, dengan x < 0 atau x > 10

Pembahasan
Koefisien fungsi kuadrat f(x) = ax2 + 2ax + 10 adalah:a = a
b = 2a
c = 10
Mari kita periksa nilai diskriminan fungsi kuadrat tersebut!
D = b2 − 4ac
= (2a)2 − 4×a×10
= 4a2 − 40a
Pembuat nol diskriminan tersebut adalah:
4a2 − 40a = 0
a2 − 10a = 0
a(a − 10) = 0
a = 0 atau a = 10
Sekarang perhatikan garis bilangannya!

Pada garis bilangan tersebut tampak bahwa untuk 0 < a < 10, nilai diskriminannya negatif (D < 0). Persamaan kuadrat yang diskriminannya negatif berarti definit positif atau selalu bernilai positif.
Jadi, fungsi f(x) mempunyai sifat selalu positif (B).
Soal No. 3 tentang Sistem Persamaan Linear
Jika x + 2y = 2a + 1 dan 3x − y = a + p maka 5x − 4y = ….
A. 2a + 2p − 1
B. a + p − 1
C. p − 1
D. 2p − 1
E. 2a − 1
A. 2a + 2p − 1
B. a + p − 1
C. p − 1
D. 2p − 1
E. 2a − 1
Pembahasan
Mari kita eliminasi sistem persamaan linear tersebut!3x − y = a + p |×2| 6x − 2y = 2a + 2p
x + 2y = 2a + 1 |×1| x + 2y = 2a + 1
————————— −
5x − 4y = 2p − 1
Jadi, nilai dari 5x − 4y adalah 2p − 1 (D).
Soal No. 4 tentang Matriks
Jika
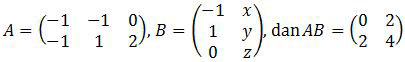
maka nilai z − x adalah ….
A. 6
B. 3
C. 0
D. −3
E. −6
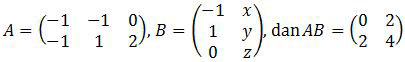
maka nilai z − x adalah ….
A. 6
B. 3
C. 0
D. −3
E. −6
Pembahasan
Modal utama untuk menyelesaikan soal di atas adalah kemampuan mengalikan dua matriks.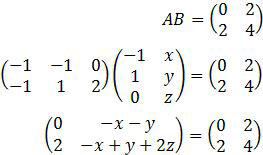
Bentuk terakhir adalah kesamaan matriks, di mana komponen-komponen yang bersesuaian nilainya sama. Kita ambil komponen kanan atas dan kanan bawah.
−x − y = 2 [komponen kanan atas]
−x + y + 2z = 4 [komponen kanan bawah]
—————— +
−2x + 2z = 6
−x + z = 3 [kedua ruas dibagi 2]
z − x = 3 [ditukar tempat menyesuaikan pertanyaan]
Jadi, nilai z − x adalah 3 (B).
Soal No. 5 tentang Peluang Kejadian
Satu dadu dilempar 3 kali. Peluang mata dadu 6 muncul sedikitnya sekali adalah ….
A. 1/216
B. 3/216
C. 12/216
D. 18/216
E. 91/216
A. 1/216
B. 3/216
C. 12/216
D. 18/216
E. 91/216
Pembahasan
Banyak semua kemungkinan sebuah dadu dilempar 3 kali adalah:n(S) = 6 × 6 × 6
= 216
Kejadian mata dadu 6 muncul sedikitnya sekali berarti mata dadu 6 diharapkan selalu muncul dari salah satu dadu, 2 dadu, atau ketiga dadu dalam setiap kali pelemparan.
Jika A adalah kejadian mata dadu 6 muncul sedikitnya sekali maka Ac adalah kejadian mata dadu 6 tidak muncul sama sekali dalam setiap pelemparan.
- pelemparan I : muncul mata dadu 1, 2, 3, 4, 5 (5 kemungkinan)
- pelemparan II : muncul mata dadu 1, 2, 3, 4, 5 (5 kemungkinan)
- pelemparan III : muncul mata dadu 1, 2, 3, 4, 5 (5 kemungkinan)
∴ n(Ac) = 5 × 5 × 5
= 125
n(A) = n(S) − n(Ac)Dengan demikian, peluang kejadian A adalah:
= 216 − 125
= 91
P(A) = n(A)/n(S)Jadi, peluang mata dadu 6 muncul sedikitnya sekali adalah 91/216 (E).
= 91/216
Pembahasan Matematika Dasar No. 6 - 10 TKPA SBMPTN 2014
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan