Pembahasan Matematika Dasar No. 6 - 10 TKPA SBMPTN 2014 Kode Naskah 642

Pembahasan soal Tes Kemampuan dan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2014 kode naskah 642 mata uji Matematika Dasar nomor 6 sampai dengan nomor 10 tentang:

• komposisi dan invers fungsi, 
• statistika, 
• logaritma, 
• fungsi kuadrat, serta 
• turunan fungsi.

Soal No. 6 tentang Komposisi dan Invers Fungsi

Jika

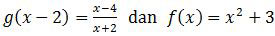
maka (f ∘ g⁻¹)(2) = ….

A.   103
B.   104
C.   130
D.   134
E.   143

Pembahasan

Langkah pertama adalah mengubah fungsi g(x − 2) menjadi fungsi g(x). Caranya dengan memanipulasi x − 4 dan x + 2 sebagai berikut: 

x − 4 = x − 2 − 2 
x + 2 = x − 2 + 4

sehingga diperoleh:

Selanjutnya, kita tentukan invers fungsi g(x) dengan menggunakan rumus

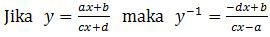
Berdasarkan rumus tersebut diperoleh:

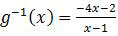
Nilai invers fungsi g untuk x = 2 adalah:


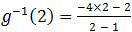
                = −10

Dengan demikian, nilai dari (f ∘ g⁻¹)(2) adalah:

(f ∘ g⁻¹)(2) = f [g⁻¹(2)]
                   = f (−10)
                   = (−10)² + 3    [f(x) = x² + 10]
                   = 100 + 3
                   = 103

Jadi nilai dari (f ∘ g⁻¹)(2) adalah 103 (A).

Soal No. 7 tentang Statistika

Tiga puluh data mempunyai rata-rata p. Jika rata-rata 20% data di antaranya adalah p + 0,1, 40% data lainnya adalah p − 0,1, 10% lainnya lagi adalah p − 0,5. Dan rata-rata 30% data sisanya adalah p + q maka q = ….

A.   1/5
B.   7/30
C.   4/15
D.   3/10
E.   1/3

Pembahasan

Data-data yang diketahui pada soal:

  n = 30
  x = p
n₁ = 20% × 30 = 6 
x₁ = p + 0,1 
n₂ = 40% × 30 = 12 
x₂ = p − 0,1 
n₃ = 10% × 30 = 3 
x₃ = p − 0,5 
n₄ = 30% × 30 = 9 
x₄ = p + q
 
Kita gunakan rumus rata-rata gabungan untuk menyelesaikan soal di atas.


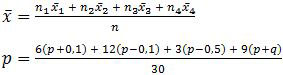
30p = 6p + 0,6 + 12p − 1,2 + 3p − 1,5 + 9p + 9q 
30p = 30p + 0,6  − 2,1 + 9q
  9q = 2,1
    q = 2,1/9
       = 21/90
       = 7/30

Jadi, nilai q pada data tersebut adalah 7/30 (B).

Soal No. 8 tentang Logaritma

Jika p = (^alog ⁡2)(^a2blog ⁡4) maka 1/p = ….

A.   2²log ⁡a + ²log ⁡√a ²log ⁡b
B.   2²log ⁡a + ½ ²log (⁡ab)
C.   (²log ⁡a)² + ½ ²log ⁡a ²log ⁡b
D.   (²log ⁡a)² + ½ ²log (⁡ab)
E.   (²log ⁡a)² + ½ ²log ⁡⁡√ab

Pembahasan

Mari kita selesaikan soal di atas dengan cermat dan hati-hati.

   p = ^alog ⁡2 . ^a2blog ⁡4
1/p = ²log a . ⁴log ⁡a²b                [tinggal dibalik]
      = ²log a (⁴log ⁡a² + ⁴log b)    [log ab = log a + log b]
      = ²log a (²²log ⁡a² + ²²log b)
      = ²log a (²log ⁡a + ½ ²log b)   [^anlog b^m = m/n ^alog ⁡b]
      = (²log ⁡a)² + ½ ²log ⁡a ²log ⁡b
 
Jadi, nilai 1/p dari bentuk logaritma tersebut adalah opsi (C).

Soal No. 9 tentang Fungsi Kuadrat

Fungsi kuadrat f(x) = x² + 2px + p mempunyai nilai minimum −p dengan p ≠ 0. Jika sumbu simetri kurva f adalah x = a maka nila a + f(a) = ….

A.   6
B.   4
C.   −4
D.   −5
E.   −6

Pembahasan

Koefisien fungsi kuadrat f(x) = x² + 2px + p adalah: 

a = 1 
b = 2p 
c = p

Sumbu simetri kurva f adalah x = a, diperoleh:


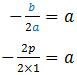
         a = −p
 
Fungsi kuadrat f mempunyai nilai minimum −p. Sedangkan nilai minimum terjadi saat x = a (sumbu simetri) sehingga diperoleh:

              f(a) = −p
a² + 2pa + p = −p
p² − 2p² + p = −p      [substitusi a = −p]
      −p² + 2p = 0
        p² − 2p = 0
       p(p − 2) = 0  
p = 0 (tidak memenuhi) atau p = 2

Dengan demikian, 

a + f(a) = −p + (−p)
             = −2p
             = −2×2
             = −4


Jadi, nilai dari a + f(a) adalah −4 (C).

Soal No. 10 tentang Turunan Fungsi

Jika m dan n bilangan real dan fungsi f(x) = mx³ + 2x² − nx + 5 memenuhi f'(1) = f'(−5) = 0 maka 3m − n = ….

A.   −6
B.   −4
C.   −2
D.   2
E.   4

Pembahasan

Mari kita turunan fungsi f(x) di atas! 

f(x) = mx³ + 2x² − nx + 5 
f'(x) = 3mx² + 4x − n

Turunan fungsi tersebut memenuhi f'(1) = f'(−5) = 0. Ambil saja f'(1) = 0.

                     f'(1) = 0
3m×1² + 4×1 − n = 0
          3m + 4 − n = 0
                 3m − n = −4

Jadi, nilai dari 3m − n adalah −4 (B).

Pembahasan Matematika Dasar No. 1 - 5 TKD Saintek SBMPTN 2014
Pembahasan Matematika Dasar No. 11 - 15 TKD Saintek SBMPTN 2014

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.