- matriks,
- fungsi kuadrat (parabola),
- pertidaksamaan,
- trigonometri, serta
- barisan dan deret.
Soal No. 11 tentang Matriks
Diketahui matriks
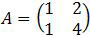
Jika |A| menyatakan determinan A maka nilai a yang memenuhi 2log a = 2|A| adalah ….
A. 1/16
B. 1/4
C. 4
D. 16
E. 32
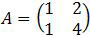
Jika |A| menyatakan determinan A maka nilai a yang memenuhi 2log a = 2|A| adalah ….
A. 1/16
B. 1/4
C. 4
D. 16
E. 32
Pembahasan
Kita tentukan determinan matriks A terlebih dahulu.|A| = ad − bc
= 1×4 − 2×1
= 4 − 2
= 2
Selanjutnya kita selesaikan persamaan logaritma tersebut.
2log a = 2|A|
2log a = 22
2log a = 4
a = 24 [jika nlog x = y maka x = ny]
= 16
Jadi, nilai a yang memenuhi 2log a = 2|A| adalah 16 (D).
Soal No. 12 tentang Fungsi Kuadrat (Parabola)
Titik-titik P dan Q masing-masing mempunyai absis 2p dan −3p terletak pada parabola y = x2 − 1. Jika garis g tegak lurus PQ dan menyinggung parabola tersebut maka garis g memotong sumbu y di titik berordinat ….



Pembahasan
Titik P mempunyai absis x = 2p dan titik Q mempunyai absis x = −3p yang terletak pada parabola y = x2 − 1. Ordinat titik P dan Q dapat diperoleh dengan melakukan substitusi x pada parabola tersebut.Titik P: x = 2p → y = 4p2 − 1
Titik Q: x = −3p → y = 9p2 − 1
Gradien garis PQ (m1) dapat diperoleh dengan rumus:
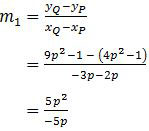
= −p
Garis g tegal lurus garis PQ, berarti perkalian gradien garis g (m2) dengan gradien garis PQ adalah −1.
m1 . m2 = −1
−p . m2 = −1
m2 = 1/p
Sehingga persamaan garis g adalah:
y = m2x + c
= x/p + c
Garis g ini memotong sumbu y (x = 0) pada ordinat:
y = c
Sekarang kita tinggal mencari nilai c.
Garis g menyinggung kurva parabola y = x2 − 1. Syarat menyinggung adalah:
- persamaan parabola = persamaan garis
x2 − 1 = x/p + c
x2 − x/p − 1 − c = 0
px2 − x − p − pc = 0 [kedua ruas dikalikan p]
- diskriminan sama dengan nol
D = 0Jadi, ordinat titik potong garis g terhadap sumbu y adalah opsi (C).
b2 − 4ac = 0
(−1)2 − 4.p.(−p − pc) = 0
1 + 4p2 + 4p2c = 0
4p2c = −1 − 4p2
Soal No. 13 tentang Pertidaksamaan
Penyelesaian pertidaksamaan
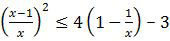
adalah ….
A. x ≤ −½
B. x ≥ −½
C. x ≥ 2
D. x ≤ 2
E. x ≤ −½ atau x ≥ 2
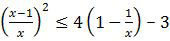
adalah ….
A. x ≤ −½
B. x ≥ −½
C. x ≥ 2
D. x ≤ 2
E. x ≤ −½ atau x ≥ 2
Pembahasan
Mari kita selesaikan soal pertidaksamaan kuadrat di atas dengan cermat dan hati-hati.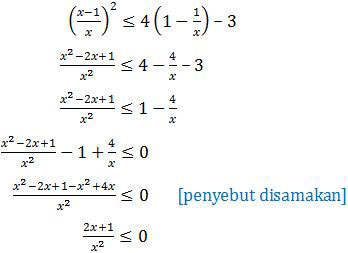
Pembuat nol pertidaksamaan tersebut adalah x = 0, x = 0, dan x = −½. Karena x = 0 ada 2 maka di sebelah kiri dan kanan 0 (pada garis bilangan) polaritasnya sama.

Jadi, penyelesaian pertidaksamaan tersebut adalah x ≤ −½ (A).
Soal No. 14 tentang Trigonometri
Jika cos 𝑥 = 2sin 𝑥 maka nilai sin 𝑥 cos 𝑥 adalah ….
A. 1/5
B. 1/4
C. 1/3
D. 2/5
E. 2/3
A. 1/5
B. 1/4
C. 1/3
D. 2/5
E. 2/3
Pembahasan
Kita manfaatkan data yang diketahui pada soal.cos 𝑥 = 2sin 𝑥
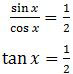
Kemudian kita buat segitiga siku-siku untuk tan x = ½.
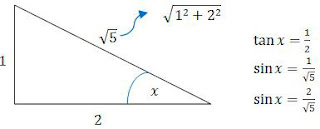
Dengan demikian,

Jadi, nilai dari sin 𝑥 cos 𝑥 adalah 2/5 (D).
Soal No. 15 tentang Barisan dan Deret
Jika 𝑎1, 𝑎2, 𝑎3 adalah barisan aritmetika dan 𝑎1, 𝑎2, 𝑎1 + 𝑎3 adalah barisan geometri maka 𝑎3/𝑎1 = ….
A. 6
B. 4
C. 3
D. 2
E. 1
A. 6
B. 4
C. 3
D. 2
E. 1
Pembahasan
Mari kita selesaikan soal di atas dengan menggunakan rumus suku tengah.- Deret aritmetika:
"2 kali suku tengah sama dengan penjumlahan suku pinggir."
- Deret geometri:
"Kuadrat suku tengah sama dengan perkalian suku pinggir'.𝑎1, 𝑎2, 𝑎3 adalah barisan aritmetika, berlaku:
2𝑎2 = 𝑎1 + 𝑎3 ... (1)
𝑎1, 𝑎2, 𝑎1 + 𝑎3 adalah barisan geometri, berlaku:
𝑎22 = 𝑎1.(𝑎1 + 𝑎3)
𝑎22 = 𝑎1.2𝑎2 [substitusi persamaan (1)]
𝑎2 = 2𝑎1 .... (2)
Sekarang kita substitusikan persamaan (2) ke persamaan (1).
2𝑎2 = 𝑎1 + 𝑎3
2(2𝑎1) = 𝑎1 + 𝑎3
4𝑎1 = 𝑎1 + 𝑎3
3𝑎1 = 𝑎3
𝑎1/𝑎3 = 1/3
𝑎3/𝑎1 = 3
Jadi, nilai dari 𝑎3/𝑎1 adalah 3 (C).
Pembahasan Matematika Dasar No. 6 - 10 TKD Saintek SBMPTN 2014
Simak juga:
Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2015
Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2016
Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2017
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

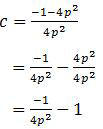
thx bgttt
ReplyDeleteSama-sama. Semoga berkaah dan manfaat
Delete