Pembahasan Matematika Dasar No. 51 - 55 TKPA SBMPTN 2015 Kode Naskah 602

Pembahasan soal Tes Kemampuan dan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2015 kode naskah 602 subtes Matematika Dasar nomor 51 sampai dengan nomor 55 tentang:

• pertidaksamaan, 
• fungsi dan komposisi fungsi, 
• sistem persamaan linear, 
• operasi aljabar, serta 
• invers fungsi.

Soal No. 51 tentang Pertidaksamaan

Himpunan penyelesaian pertidaksamaan

adalah ….

A.   {x ∈ R│x < 0}
B.   {x ∈ R│−1 < x < 0}
C.   {x ∈ R│0 < x < 1}
D.   {x ∈ R│x < −2 atau x > 1}
E.   {x ∈ R│x < −1 atau x > 0}

Pembahasan

Dalam menyelesaikan soal pertidaksamaan, jangan sekali-kali mengalikan silang, membagi, mengalikan dengan variabel, kecuali jika variabel tersebut definit positif. Penyelesaian yang paling aman adalah dengan memindah ruas.

Dalam pertidaksamaan pecahan, berlaku hubungan:

Jika a/b < 0 maka a.b < 0

Sehingga pertidaksamaan di atas menjadi: 

x(2x + 2) < 0

Pembuat nol pertidaksamaan tersebut adalah: 

x = 0
2x + 2 = 0 → x = −1

Karena koefisien kuadratnya positif (2x²) maka tanda "<" berarti penyelesaian pertidaksamaan tersebut berada di antara titik pembuat nol.

−1 < x < 0

Jadi, himpunan penyelesaian pertidaksamaan tersebut adalah opsi (B).

Soal No. 52 tentang Fungsi dan Komposisi Fungsi

Diketahui suatu fungsi f bersifat f(−x) = −f(x) untuk setiap bilangan real x. Jika f(3) = −5 dan f(−5) = 1 maka f(f(−3)) = ….

A.   −5
B.   −2
C.   −1
D.   1
E.   2

Pembahasan

Data-data yang diketahui pada soal: 

f(−x) = −f(x) 
f(3) = −5 
f(−5) = 1

Sekarang kita langsung masuk ke pertanyaan. 

f(f(−3)) = f(−f(3))    [f(−x) = −f(x)]
             = −f(f(3))    [f(3) = −5]
             = −f(−5)      [f(−5) = 1]
             = −1

Jadi, nilai dari f(f(−3)) adalah −1 (C).

Soal No. 53 tentang Sistem Persamaan Linear

Diketahui sistem persamaan linear

Nilai x + y adalah ....

A.   −3
B.   −2
C.   −1
D.   3
E.   5

Pembahasan

Sistem persamaan linear di atas kita sederhanakan dengan mengalikan 6 pada masing-masing ruas.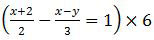


3(x + 2) − 2(x − y) = 6
   3x + 6 − 2x + 2y = 6
                    x + 2y = 0      ... (1)


2(x + y) − 3(y + 1) = 12
    2x + 2y − 3y − 3 = 12
                     2x − y = 15    ... (2)

Sekarang kita eliminasi persamaan (1) dan (2). 

x + 2y = 0     |×2|  2x + 4y = 0
2x − y = 15   |×2|  2x −  y  = 15
                          —————— −
                                      5y = −15
                                        y = −3

Selanjutnya kita substitusi y = −3 ke persamaan (1). 

y = −3 → x + 2y = 0
                  x − 6 = 0
                        x = 6

Dengan demikian, 

x + y = 6 − 3
         = 3

Jadi, nilai dari x + y adalah 3 (C).

Soal No. 54 tentang Operasi Aljabar

Empat orang siswa akan mengikuti suatu perlombaan karya inovatif. Untuk itu, diperlukan biaya Rp900.000,00. Karena masing-masing memiliki kondisi keuangan berbeda, besar kontribusi masing-masing siswa tidak sama. Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya. Siswa B memberikan kontribusi sepertiga dari jumlah kontribusi tiga siswa lainnya. Siswa C memberikan kontribusi seperempat dari jumlah kontribusi tiga siswa lainnya. Besar kontribusi siswa D adalah Rp ….

A.   150.000,00
B.   180.000,00
C.   195.000,00
D.   225.000,00
E.   300.000,00

Pembahasan

Empat orang siswa (A, B, C, dan D) akan mengikuti lomba karya inovatif dengan biaya Rp900.000,00. Biaya tersebut ditanggung bersama.

A + B + C + D = 900.000

Siswa A memberikan kontribusi setengah dari jumlah kontribusi tiga siswa lainnya.

  A = ½(B + C + D)
  A = ½(900.000 − A) [kedua ruas dikalikan 2]
2A = 900.000 − A
3A = 900.000
  A = 300.000

Siswa B memberikan kontribusi sepertiga dari jumlah kontribusi tiga siswa lainnya.

  B = ⅓(A + C + D)
  B = ⅓(900.000 − B)  [kedua ruas dikalikan 3]
3B = 900.000 − B
4A = 900.000
  A = 225.000

Siswa C memberikan kontribusi seperempat dari jumlah kontribusi tiga siswa lainnya.

  C = ¼(A + B + D)
  C = ¼(900.000 − C) [kedua ruas dikalikan 4]
4C = 900.000 − C
5C = 900.000
  C = 180.000

Dengan demikian, besar kontribusi siswa D adalah:

D = 900.000 − (A + B + C)
    = 900.000 − (300.000 + 225.000 + 180.000)
    = 900.000 − 705.000
    = 195.000

Jadi, besar kontribusi siswa D adalah Rp195.000,00 (C).

Soal No. 55 tentang Invers Fungsi

Jika

maka f⁻¹(x) = ....

Pembahasan

Langkah pertama adalah mengubah bentuk f(x + 2) menjadi bentuk f(x).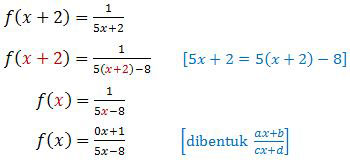

Selanjutnya kita tentukan invers fungsi f(x) dengan menggunakan rumus:

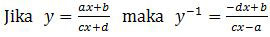
Dengan menggunakan rumus invers di atas, diperoleh:

Jadi, invers fungsi f adalah opsi (B).

Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2015
Pembahasan Matematika Dasar No. 56 - 60 TKPA SBMPTN 2015

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.