Pembahasan Matematika Dasar No. 56 - 60 TKPA SBMPTN 2015 Kode Naskah 602

Pembahasan soal Tes Kemampuan dan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2015 kode naskah 602 subtes Matematika Dasar nomor 56 sampai dengan nomor 60 tentang:

• matriks, 
• persamaan dan fungsi kuadrat, 
• grafik fungsi kuadrat, 
• ukuran pemusatan, serta 
• peluang kejadian.

Soal No. 56 tentang Matriks

Jika

merupakan matriks yang mempunyai invers maka jumlah semua nilai a yang mungkin sehingga det (−½ A) = det (A⁻¹) adalah ….

A.   2
B.   4
C.   6
D.   8
E.   10

Pembahasan

Rumus determinan matriks yang perlu dikuasai untuk menjawab soal di atas adalah:

det (kA) = k² det A
det A⁻¹ = 1/(det A)

Determinan untuk matriks A di atas adalah:

det A = 2a − 6

Mari kita kerjakan soal di atas!

 det (−½ A) = det (A⁻¹)
(−½)² det A = 1/(det A)
      ¼ det A = 1/(det A)
      (det A)² = 4

Sekarang kita masukkan det A = 2a − 6.

          (2a − 6)² = 4
4a² − 24a + 36 = 4
4a² − 24a + 32 = 0
      a² − 6a + 8 = 0

Karena berbentuk persamaan kuadrat, maka nilai a ada dua, yaitu a₁ dan a₂. Untuk mendapatkan jumlah nilai a, kita bisa menggunakan rumus jumlah akar-akar persamaan kuadrat. 

a₁ + a₂ = −b/a             [a = 1, b = −6]
             = − (−6)/1
             = 6

Jadi, jumlah semua nilai a yang mungkin adalah 6 (C).

Soal No. 57 tentang Persamaan dan Fungsi Kuadrat

Diketahui titik minimum fungsi kuadrat y = x² + bx + c adalah (5/2, −1/4). Jika grafik fungsi tersebut melalui titik (p, 0) dan (q, 0) maka nilai p²q + pq² adalah ….

A.   −30
B.   −11
C.   11
D.   25
E.   30

Pembahasan

Absis titik minimum fungsi kuadrat adalah sumbu simetri.

   x = −b/2a    [rumus sumbu simetri]
5/2 = −b/2      [a = 1]
   b = −5

Untuk mendapatkan nilai c, kita substitusikan titik minimum (5/2, −1/4) dan b = −5 pada fungsi kuadrat tersebut.

      y = x² + bx + c
−1/4 = (5/2)² + (−5)(5/2) + c
−1/4 = 25/4 −25/2 + c
   −1 = 25 − 50 + 4c    [kedua ruas dikalikan 4]
   24 = 4c
     c = 6

Dengan ditemukannya nilai b dan c, persamaan kuadrat tersebut menjadi: 

y = x² − 5x + 6

Grafik fungsi kuadrat tersebut melalui titik (p, 0) dan (q, 0). Kedua titik ini merupakan titik potong pada sumbu x atau pembuat nol fungsi sehingga p dan q merupakan akar-akar persamaan kuadrat tersebut.

Mari kita gunakan sifat penjumlahan dan perkalian akar-akar persamaan kuadrat. 

p + q = −b/a    [a = 1, b = −5]
          = 5 

p . q = c/a         [a = 1, c = 6]
        = 6

Dengan demikian, nilai dari p²q + pq² adalah: 

p²q + pq² = pq(p + q)
                = 6 × 5
                = 30

Jadi, nilai dari adalah 30 (E).

Soal No. 58 tentang Grafik Fungsi Kuadrat

Jika grafik fungsi y = 4 − x² memotong sumbu-x di titik A dan B serta memotong sumbu-y di titik C, maka luas segitiga ABC adalah ….

A.   2
B.   4
C.   6
D.   8
E.   9

Pembahasan

Grafik fungsi y = 4 − x² memotong sumbu-x di titik A dan B.

       y = 0
4 − x² = 0
      x² = 4
        x = ±2
∴ A(−2, 0) dan B(2, 0)

Grafik fungsi y = 4 − x² memotong sumbu-y di titik C. 

x = 0 → y = 4 − x²
               y = 4 − 0²
               y = 4
∴ C(0, 4)

Perhatikan ilustrasi grafik yang dimaksud pada soal berikut ini!

Berdasarkan grafik di atas, luas segitiga ABC adalah:

L ΔABC = ½ × AB × OC
               = ½ × 4 × 4
               = 8

Jadi, luas segitiga ABC adalah 8 satuan luas (D).

Soal No. 59 tentang Ukuran Pemusatan

Suatu perusahaan memproduksi dua jenis produk. Penjualan produk tersebut dilakukan oleh agen yang telah ditunjuk. Untuk penjualan produk A terdapat 20 agen, sedangkan untuk penjualan produk B ada 40 agen. Total keuntungan semua agen dalam satu bulan terakhir sebesar 360 juta rupiah. Jika rata-rata keuntungan agen yang menjual produk A adalah sebesar dua kali rata-rata keuntungan agen yang menjual produk B, maka rata-rata keuntungan agen yang menjual produk A adalah ….

A.   2,4 juta rupiah
B.   3 juta rupiah
C.   3,6 juta rupiah
D.   6 juta rupiah
E.   9 juta rupiah

Pembahasan

Data-data yang diketahui pada soal: 

n_A = 20 
n_B = 40 
x_A = 2x_B → x_B = ½ x_A

Total keuntungan agen A dan B sebesar 360 juta rupiah.

    n_A . x_A + n_B . x_B = 360
20 . x_A + 40 . ½ x_A = 360
          20x_A + 20x_A = 360
                       40x_A = 360
                           x_A = 9

Jadi, rata-rata keuntungan agen yang menjual produk A adalah 9 juta rupiah (E).

Soal No. 60 tentang Peluang Kejadian

Empat buku berjudul Kombinatorika dan dua buku berjudul Statistika akan disusun di lemari buku dalam satu baris. Misalkan C adalah kejadian susunan buku sehingga terdapat tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Jika buku dengan judul yang sama tidak dibedakan maka peluang kejadian C adalah ….

A.   4/5
B.   2/3
C.   3/5
D.   1/2
E.   1/5

Pembahasan

Terdapat 6 buku, yaitu 4 buku Kombinatorika dan 2 buku Statistika disusun dengan tidak membedakan judul yang sama. Banyak semua kemungkinan (ruang sampel) dapat ditentukan dengan menggunakan permutasi dengan unsur yang sama. 

n(S) = ₆P_{(4, 2)}       

      
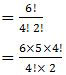
       = 15

C adalah kejadian susunan buku sehingga terdapat tiga atau lebih buku dengan judul yang sama tersusun secara berurutan. Susunan yang mungkin adalah:

• KKKKSS   [huruf bercetak merah diacak]

3!/2! = 3     [permutasi 3 dengan 2 unsur yang sama]

• SSKKKK   

3!/2! = 3   

• Tiga atau lebih buku Kombinatorika ada di tengah

1. SKKKKS
2. SKKKSK
3. KSKKKS

Sehingga banyak kejadian C adalah: 

n(C) = 3 + 3 + 3
        = 9

Peluang kejadian C adalah: 

P(C) = n(C)/n(S)
         = 9/15
         = 3/5

Jadi, peluang kejadian C adalah 3/5 (C).

Pembahasan Matematika Dasar No. 51 - 55 TKPA SBMPTN 2015

Simak juga:
Pembahasan Matematika Dasar No. 1 - 5 TKPA SBMPTN 2014
Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2016
Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2017

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.