Pembahasan Matematika SMP UN 2016 No. 26 - 30

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2016 nomor 26 sampai dengan nomor 30 tentang:

• luas segitiga, 
• penerapan keliling bangun datar, 
• teorema Pythagoras, 
• unsur-unsur bangun ruang, dan 
• kerangka bangun ruang.

Soal No. 26 tentang Luas Segitiga

Perhatikan gambar berikut!

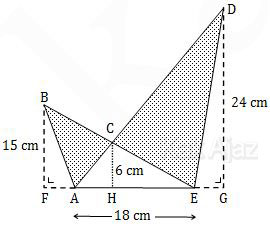
Luas daerah yang diarsir adalah ….

A.   297 cm²
B.   279 cm²
C.   243 cm²
D.   234 cm²

Pembahasan

Luas daerah yang diarsir adalah:

L = L.∆AEB + L.∆AED − 2×L.∆AEC
   = ½ ∙ 18 ∙ 15 + ½ ∙ 18 ∙ 24 − 2 ∙ ½ ∙ 18 ∙ 6
   = ½ ∙ 18(15 + 24 − 12)
   = 9 ∙ 27
   = 243

Jadi, luas daerah yang diarsir adalah 243 cm² (C).

Soal No. 27 tentang Penerapan Keliling Bangun Datar

Guntur memiliki sebidang tanah berbentuk persegi panjang berukuran 60 m × 40 m. Di sekeliling tanah akan ditanami pohon dengan jarak antarpohon 2 meter yang dimulai dari salah satu sudutnya. Jika harga tiap pohon Rp35.000,00, biaya pembelian pohon seluruhnya adalah ….

A.   Rp84.000.000,00
B.   Rp48.000.000,00
C.   Rp7.000.000,00
D.   Rp3.500.000,00

Pembahasan

Keliling tanah milik Guntur adalah:

K = 2(p + l)
    = 2(60 + 40) m
    = 200 m

Di sekeliling tanah tersebut akan ditanami pohon dengan jarak antarpohon 2 meter.

Banyak pohon =200 ∶ 2
                       =100 pohon

Harga 1 pohon adalah Rp35.000,00. Harga seluruh pohon adalah:

   Rp35.000,00 × 100
= Rp3.500.000,00

Jadi, biaya pembelian pohon seluruhnya adalah Rp3.500.000,00 (D).

Soal No. 28 tentang Teorema Pythagoras

Sebuah kapal berlayar sejauh 45 km ke arah timur, kemudian berbelok ke arah utara sejauh 60 km. Jarak terpendek yang dilalui kapal dari titik awal adalah ….

A.   45 km
B.   60 km
C.   75 km
D.   80 km

Pembahasan

Berikut ini gambar ilustrasi untuk soal tersebut.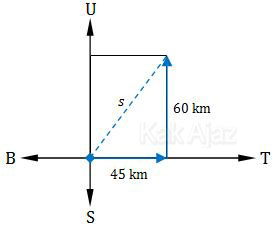

Berdasarkan ilustrasi di atas, jarak terpendek (s) dapat ditentukan dengan teorema Pythagoras.

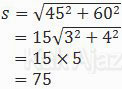
Jadi, jarak terpendek yang dilalui kapal dari titik awal adalah 75 km (C).

Soal No. 29 tentang Unsur-unsur Bangun Ruang

Perhatikan gambar kubus berikut!

Bidang diagonal yang tegak lurus dengan ABGH adalah ….
A.   EFGH
B.   DCGH
C.   CDEF
D.   EBCH

Pembahasan

Perhatikan bidang diagonal berikut ini!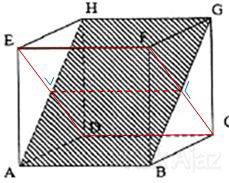

Jadi, bidang diagonal yang tegak lurus dengan ABGH adalah CDEF (C).

Soal No. 30 tentang Kerangka Bangun Ruang

Mumtaz membuat kerangka akuarium yang terbuat dari aluminium dengan ukuran 120 cm × 60 cm × 80 cm. Jika harga 1 meter aluminium Rp8.000,00, biaya yang diperlukan untuk membeli aluminium adalah ….

A.   Rp41.600,00
B.   Rp57.600,00
C.   Rp83.200,00
D.   Rp94.200,00

Pembahasan

Akuarium tersebut berbentuk balok. Jumlah rusuk balok ada 12 yang terdiri dari 4 panjang, 4 lebar, dan 4 tinggi.

Panjang aluminium yang dibutuhkan sama dengan jumlah panjang semua rusuk balok.

Panjang rusuk = 4(p + l + t)
                       = 4(120 + 60+80) cm
                       = 4 × 260 cm
                       = 1040 cm
                       = 10,4 m

Sementara itu, harga 1 meter aluminium Rp8.000,00.

Biaya = Rp8.000,00 × 10,4
          = Rp83.200,00

Jadi, biaya yang diperlukan untuk membeli aluminium adalah Rp83.200,00 (C).

Simak Pembahasan Soal Matematika SMP UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.