Pembahasan Matematika IPA UN: Sudut antara Dua Vektor

Pembahasan soal-soal Ujian Nasional (UN) SMA-IPA bidang studi Matematika dengan materi pembahasan Sudut antara Dua Vektor yang meliputi:

• besar sudut antara dua vektor, 
• nilai sinus atau kosinus sudut antara dua vektor.

Soal tentang Sudut antara Dua Vektor UN 2012

Diketahui titik A(1, 0, −2), B(2, 1, −1), dan C(2, 0, −3). Sudut antara vektor AB dengan AC adalah ….

A.   30°
B.   45°
C.   60°
D.   90°
E.   120°

Pembahasan

Langkah pertama kita tentukan komponen vektor AB dan vektor AC.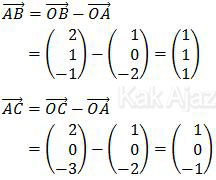

Selanjutnya kita gunakan rumus sudut antara dua vektor.

Jadi, sudut antara vektor AB dengan vektor AC adalah 90° (D).

Soal tentang Sudut antara Dua Vektor UN 2010

Diketahui vektor-vektor:

u = i + √2 j + √5 k
v = i − √2 j + √5 k

Sudut antara vektor u dan v adalah ….

A.   30°
B.   45°
C.   60°
D.   90°
E.   120°

Pembahasan

Untuk menentukan sudut antara vektor u dan v kita perlu menghitung perkalian kedua vektor tersebut dan panjang masing-masing vektor.

u ∙ v = 1∙1 + √2∙(−√2) + √5∙√5
        = 1 − 2 + 5
        = 4

|u| = √[1² + (√2)² + (√5)²]
    = √8

|v| = √[1² + (−√2)² + (√5)²]
    = √8

Sudut antara vektor u dan v dirumuskan sebagai:

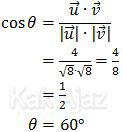
Jadi, Sudut antara vektor u dan v adalah 60° (C).

Soal tentang Sudut antara Dua Vektor UN 2013

Diketahui vektor p = i + j − 4k dan q = −2i − j. Nilai sinus sudut antara vektor p dan q adalah ….

A.   −3/10 √10
B.   −1/10 √10
C.   1/10 √10
D.   1/3 √10
E.   3/10 √10

Pembahasan

Kita tentukan dulu operasi vektor yang diperlukan.

p ∙ q = −2 − 1 + 0
        = −3

|p| = √[1² + 1² + (−4)²]
     = √18
     = 3√2

|q| = √[(−2)² + (−1)²]
     = √5

Sudut antara vektor p dan q dirumuskan sebagai:

Untuk mendapatkan nilai sinus sudut, kita gunakan rumus identitas trigonometri.

sin²⁡ θ = 1 − cos²⁡ θ
          = 1 − 1/10
          = 9/10
  sin⁡θ = ±3/(√10) 
          = ±3/10 √10 (kuadran II atau III)

Teks soal tidak menyebutkan interval sudut. Bila yang dimaksud kuadran II maka jawabannya +3/10 √10, sedangkan bila yang dimaksud kuadran III maka jawabannya adalah −3/10 √10.

Jadi, nilai sinus sudut antara vektor p dan q adalah ±3/10 √10 (A/E).

Soal tentang Sudut antara Dua Vektor UN 2015

Diketahui |a| = 4, |b| = 6, |a + b| = 8. Jika θ adalah sudut antara vektor a dan b maka nilai dari cos⁡ 2θ adalah ….

A.   −7/8
B.   −3/4
C.   0
D.   1/2
E.   1

Pembahasan

Panjang vektor a + b merupakan resultan dari penjumlahan vektor a dan b sehingga berlaku:

 |a + b|² = |a|² + |b|² + 2|a||b| cos⁡ θ
         8² = 4² + 6² + 2∙4∙6 cos ⁡θ
         64 = 52 + 48 cos⁡ θ
48 cos ⁡θ = 12
     cos ⁡θ = 1/4

Karena yang ditanyakan nilai dari cos⁡ 2θ maka kita gunakan rumus kosinus sudut ganda.

cos⁡ 2θ = 2 cos²⁡ θ − 1
           = 2 (1/4)² − 1
           = 1/8 − 1
           = −7/8

Jadi, nilai dari cos⁡ 2θ adalah −7/8 (A).

Soal tentang Sudut antara Dua Vektor UN 2014

Diketahui vektor-vektor u = ai + 9j + bk dan v = −bi + aj + ak. Sudut antara vektor u dan v adalah θ dengan cos⁡ θ = 6/11. Proyeksi u pada v adalah p = −2i + 4j + 4k. Nilai b = ….

A.   √2
B.   2
C.   2√2
D.   4
E.   4√2

Pembahasan

Proyeksi u pada v adalah p, ini berarti bahwa vektor v adalah searah dengan vektor p atau vektor v merupakan kelipatan dari vektor p.

Dari kesamaan vektor di atas diperoleh:

−b = −2k
  k = 1/2 b

a = 4k
   = 4 ∙ 1/2 b
   = 2b

Nah, sekarang kita substitusikan a = 2b pada komponen vektor u dan v.

u = ai + 9j + bk
   = 2bi + 9j + bk

v = −bi + aj + ak
   = −bi + 2bj + 2bk

Selanjutnya kita gunakan rumus sudut antara dua vektor. Namun, sebelumnya kita tentukan dulu operasi vektor yang diperlukan pada rumus tersebut.

u ∙ v = −2b² + 18b + 2b²
        = 18b

|u| = √[(2b)² + 9² + b²]
     = √(5b² + 81)

|v| = √[(−b)² + (2b)² + (2b)²]
    = √(9b²)
    = 3b

Kita masukkan data-data di atas pada rumus sudut antara dua vektor.

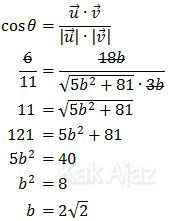
Jadi, nilai b adalah 2√2 (C).

Pembahasan soal lain tentang Sudut antara Dua Vektor bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 16
Pembahasan Matematika IPA UN 2014 No. 15
Pembahasan Matematika IPA UN 2015 No. 17

Simak juga:
Pembahasan Matematika IPA UN: Operasi Vektor
Pembahasan Matematika IPA UN: Proyeksi Vektor

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.