Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2018 Kode Naskah 466 nomor 1 sampai dengan nomor 5 tentang:
- fungsi trigonometri,
- transformasi geometri,
- dimensi tiga,
- limit fungsi, serta
- barisan dan deret.
Soal No. 1 tentang Fungsi Trigonometri
Jika nilai maksimum dan minimum fungsi f(x) = k sin(x) + c berturut-turut adalah 7 dan 3 maka nilai maksimum fungsi g(x) = 2k cos(x) + 5c adalah ….
A. 7
B. 10
C. 14
D. 20
E. 29
A. 7
B. 10
C. 14
D. 20
E. 29
Pembahasan
Diketahui:f(x)max = 7
f(x)min = 3
Nilai maksimum atau minimum fungsi trigonometri bergantung pada amplitudo (k) dan nilai konstanta (c).
Nilai maksimum terjadi saat amplitudonya positif.
f(x) = k sin(x) + c
f(x)max = +k + c
7 = +k + c … (1)
Sedangkan nilai minimum terjadi saat amplitudonya negatif.
f(x)min = −k + c
3 = −k + c … (2)
Selanjutnya kita eliminasi persamaan (1) dan (2).
7 = +k + c
3 = −k + c
⎯⎯⎯⎯⎯⎯⎯ −
4 = 2k
k = 2
Kemudian kita substitusi k = 2 ke persamaan (1).
7 = k + c
7 = 2 + c
c = 5
Dengan modal nilai k dan c yang baru saja kita peroleh, mari kita tentukan nilai maksimum dari fungsi g(x).
g(x) = 2k cos(x) + 5c
g(x)max = 2k + 5c
= 2 ∙ 2 + 5 ∙ 5
= 4 + 25
= 29
Jadi, nilai maksimum fungsi g(x) adalah 29 (E).
Soal No. 2 tentang Transformasi Geometri
Diketahui gradien garis melalui titik O(0, 0) dan P(a, b) adalah 2. Titik P dicerminkan terhadap sumbu y kemudian digeser 1 satuan ke atas dan 4 satuan ke kiri, maka gradien garis yang melalui P' dan O(0,0) adalah −1. Titik P adalah ….
A. (−2, −4)
B. (−1, −2)
C. (1, 2)
D. (2, 4)
E. (3, 6)
A. (−2, −4)
B. (−1, −2)
C. (1, 2)
D. (2, 4)
E. (3, 6)

Pembahasan
Gradien garis melalui titik O(0, 0) dan P(a, b) adalah 2.
Pencerminan terhadap sumbu y dirumuskan:
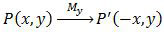
Sehingga,

Kemudian hasil pencerminan tersebut digeser 1 satuan ke atas dan 4 satuan ke kiri. Ini berarti bahwa nilai absis (x) dikurangi 4 sedangkan nilai ordinat (y) ditambah 1.

Gradien garis yang melalui titik O(0,0) dan titik P"(−a − 4, b + 1) adalah −1.
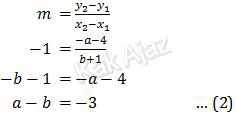
Substitusi persamaan (1) ke persamaan (2) diperoleh:
a − 2a = −3
−a = −3
a = 3
Substitusi a = 3 ke persamaan (1) diperoleh:
b = 2a
= 2 ∙ 3
= 6
Jadi, koordinat titik P(a, b) adalah P(3, 6) (E).
Soal No. 3 tentang Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2√2 cm. Jika titik P di tengah-tengah AB dan titik Q di tengah-tengah BC maka jarak antara titik H dengan garis PQ adalah … cm.
A. √15
B. 4
C. √17
D. 3√2
E. √19
A. √15
B. 4
C. √17
D. 3√2
E. √19
Pembahasan
Kubus yang dimaksud pada soal adalah:
Jarak titik H ke garis PQ adalah garis HR. Garis HR merupakan sisi tegak segitiga siku-siku HRQ. Oleh karena itu, kita perlu mencari panjang HQ dan RQ.
Pandang garis HQ pada kubus. Untuk menempuh jarak terdekat HQ pada kubus bisa melalui HG – GC – CQ. Sehingga:
HQ2 = HG2 + GC2 + CQ2
= (2√2)2 + (2√2)2 + (√2)2
= 8 + 8 + 2
= 18
Sedangkan PQ merupakan sisi miring segitiga PBQ, sehingga:
PQ = √(PB2 + BQ2)
= √[(√2)2 + (√2)2]
= √4
= 2
Panjang RQ adalah setengah dari panjang PQ.
RQ = ½ × 2
= 1
Dengan demikian, panjang HR adalah:
HR = √(HQ2 − RQ2)
= √(18 − 1)
= √17
Jadi, jarak antara titik H dengan garis PQ adalah √17 cm (C).
Soal No. 4 tentang Limit Fungsi
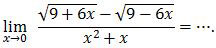
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan
Limit fungsi bentuk pecahan di atas lebih mudah diselesaikan dengan Dalil L’Hopital. Caranya dengan menurunkan pembilang dan penyebutnya.Turunan pembilang:

Turunan penyebut:
y = x2 + x
y' = 2x + 1
Dengan demikian,

Dengan melakukan substitusi x = 0, diperoleh:
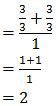
Jadi, nilai limit fungsi tersebut adalah 2 (C).
Soal No. 5 tentang Barisan dan Deret
Diketahui barisan geometri un dengan u3 + u4 = 4(u1 + u2) dan u1 u4 = 4u2. Jumlah 4 suku pertama yang mungkin adalah ….
A. −2
B. −1
C. 5
D. 10
E. 15
A. −2
B. −1
C. 5
D. 10
E. 15
Pembahasan
Suku ke-n deret geometri dirumuskan:un = arn−1
Berdasarkan rumus di atas, mari kita ulas data-data pada soal di atas. Kak Ajaz mulai dari data yang pertama.
u3 + u4 = 4(u1 + u2)
ar2 + ar3 = 4(a + ar)
r2 (a + ar) = 4(a + ar)
r2 = 4
r = ±2
Selanjutnya, kita ulas data yang kedua.
u1 u4 = 4u2
a ∙ ar3 = 4ar
ar2 = 4
Substitusi r2 = diperoleh:
a ∙ 4 = 4
a = 1
Nah, sekarang kita cari jumlah 4 suku pertama deret tersebut untuk r = 2 dan r = −2.
Untuk r = 2
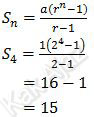
Untuk r = −2
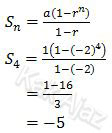
Jadi, jumlah 4 suku pertama yang mungkin adalah 15 (E).
Simak Pembahasan Soal TKD Saintek SBMPTN 2018 selengkapnya.
| No. 01 - 05 (Mat) | No. 31 - 35 (Kim) |
| No. 06 - 10 (Mat) | No. 36 - 40 (Kim) |
| No. 11 - 15 (Mat) | No. 41 - 45 (Kim) |
| No. 16 - 20 (Fis) | No. 46 - 50 (Bio) |
| No. 21 - 25 (Fis) | No. 51 - 55 (Bio) |
| No. 26 - 30 (Fis) | No. 56 - 60 (Bio) |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

Bukankah jawaban soal limit itu pembahasannya kurang tepat?
ReplyDeleteBukahkah cara l' hospotal digunakan kalo x mendekati angka selain nol?
Dalil L'Hopital adalah cara lain untuk menyelesaikan soal limit. Dalil tersebut bisa digunakan untuk menyelesaikan semua jenis soal limit.
DeleteHanya saja, tidak semua jenis soal efektif dikerjakan dengan dalil L'Hopital (bisa diselesaikan tapi langkahnya malah lebih panjang).
Dalil L'Hopital juga bisa digunakan untuk menyelesaikan soal limit mendekati nol.
Contoh: limit mendekati nol sin x dibagi x
Dengan cara yang sudah umum, hasilnya adalah 1 (lebih efektif).
Sekarang kita kerjakan dengan dalil L'Hopital:
- turunan pembilang = cos x
substitusi x = 0 hasilnya 1
-turunan penyebut = 1
Hasilnya, pembilang dibagi penyebut = 1
Bisa kan? Cuma kurang efektif