Pembahasan Matematika No. 6 - 10 TKD Saintek SBMPTN 2018 Kode Naskah 466

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2018 Kode Naskah 466 nomor 6 sampai dengan nomor 10 tentang:

• aplikasi integral, 
• kaidah pencacahan, 
• lingkaran, 
• suku banyak, dan 
• persamaan garis.

Soal No. 6 tentang Aplikasi Integral

Daerah R dibatasi oleh y = a√x , y = ax², untuk x ∈ [0, 2]. Jika volume benda padat yang didapat dengan memutar R terhadap sumbu x adalah 5π maka a = ….

A.   −5
B.   −4
C.   −3
D.   −2
E.   −1

Pembahasan

Grafik fungsi y₁ = a√x adalah parabola terbuka ke kanan, sedangkan grafik fungsi y₂ = ax² adalah parabola terbuka ke atas.

Titik potong kedua parabola tersebut adalah:

            y₁ = y₂
         a√x = ax²
           √x = ax²            [a dari kedua ruas dicoret]
             x = x⁴              [dikuadratkan]
     x⁴ − x = 0
x(x³ − 1) = 0
x = 0 atau x = 1

Dengan demikian, daerah R yang dimaksud adalah:

Daerah R terbagi dua daerah, yaitu daerah I dan II. Pada daerah I, y₁ berada di atas y₂ sedangkan pada daerah II, y₂ berada di atas y₁.

Dengan demikian, volume benda padat yang didapat dengan memutar R terhadap sumbu x adalah dapat dirumuskan:

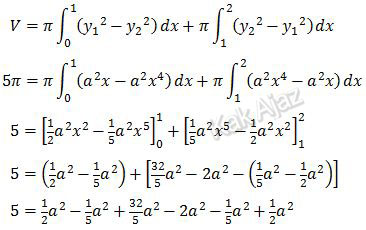
Nah, sekarang masing-masing suku kita kalikan dengan 10 kemudian kita selesaikan.

50 = 5a² − 2a² + 64a² − 20a² − 2a² + 5a²
50 = 50a²
a² = 1
  a = ±1

Jadi, sesuai opsi jawaban yang ada, nilai a pada fungsi kuadrat tersebut adalah −1 (E).

Soal No. 7 tentang Kaidah Pencacahan

Ari dan Ira merupakan anggota dari suatu kelompok yang terdiri dari 9 orang. Banyaknya cara membuat barisan dengan syarat Ari dan Ira tidak berdampingan adalah ….

A.   7×8!
B.   6×8!
C.   5×8!
D.   7×7!
E.   6×7!

Pembahasan

Barisan yang dimaksud adalah barisan memanjang yang terdiri dari 9 orang. Banyak barisan yang mungkin dapat dibuat adalah:

Bila Ari dan Ira selalu berdampingan maka banyak barisan yang terbentuk adalah:

Dengan demikian, banyaknya cara membuat barisan dengan syarat Ari dan Ira TIDAK berdampingan adalah:

   9! − 2×8!
= 9×8! − 2×8!
= (9 − 2) × 8!
= 7×8!

Jadi, banyaknya cara membuat barisan dengan syarat Ari dan Ira tidak berdampingan adalah 7 × 8! (A).

Soal No. 8 tentang Lingkaran

Jika lingkaran x² + y² − ax − ay + a = 0 mempunyai panjang jari-jari 1/2 a maka nilai a adalah ….

A.   1
B.   2
C.   3
D.   4
E.   5

Pembahasan

Bentuk umum persamaan lingkaran adalah:

x² + y² + Ax + By + C = 0

Mari kita banding persamaan lingkaran pada soal dengan bentuk umumnya.

x² + y² − ax − ay + a = 0
x² + y² + Ax + By + C = 0

Diperoleh:

A = −a
B = −a
C = a

Adapun rumus jari-jari lingkaran berdasarkan bentuk umumnya adalah:

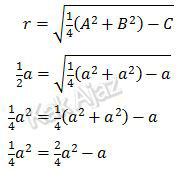
Masing-masing suku kita kalikan 4, diperoleh:

         a² = 2a² − 4a
 a² − 4a = 0
a(a − 4) = 0
a = 0 atau a = 4

Jadi, nilai a pada persamaan lingkaran tersebut adalah 4 (D).

Soal No. 9 tentang Suku Banyak

Sisa pembagian p(x) = 2x³ + x² + 2a²x + 2b + 1 oleh x² + a² adalah 4. Jika pembagian p(x) oleh x − 1 bersisa 10 maka a² + b = ….

A.   0
B.   √3
C.   3
D.   6
E.   2√3

Pembahasan

Menurut teorema sisa, jika suku banyak f(x) dibagi x − a maka sisanya adalah f(a).

Dengan demikian, suku banyak p(x) dibagi x − 1 sisanya adalah p(1). Sisa pembagian tersebut adalah 10 sehingga p(1) = 10.

p(x) = 2x³ + x² + 2a²x + 2b + 1

                                       p(1) = 10
2 ∙ 1³ + 1² + 2a² ∙ 1 + 2b + 1 = 10
                          2a² + 2b + 4 = 10
                                2a² + 2b = 6
                                    a² + b = 3

Jadi, nilai dari a² + b adalah 3 (C).

Soal No. 10 tentang Persamaan Garis

Garis yang melalui titik O(0, 0) dan P(a, b) berpotongan tegak lurus dengan garis singgung kurva y  = x² − 9/2 di P(a, b). Jika titik P berada di kuadran III maka a + b adalah ….

A.   −9/2
B.   −5/2
C.   ½(−6 − √6)
D.   ¼(−15 − 2√3)
E.   ½(−8 − √2)

Pembahasan

Gradien garis yang melalui titik O(0, 0) dan P(a, b) adalah:

Sedangkan gradien garis singgung kurva y  = x² − 9/2 di titik P(a, b) adalah:

m₂ = y'
      = 2x

Substitusi x = a diperoleh:

m₂ = 2a

Karena garis OP dan garis singgung kurva saling tegak lurus maka perkalian kedua gradiennya adalah −1.

m₁ ∙ m₂ = −1
b/a ∙ 2a = −1
        2b = −1
          b = −1/2

Untuk mendapatkan nilai a, kita substitusikan titik P(a, b) pada persamaan kurva.

(a, b) → y  = x² − 9/2
              b  = a² − 9/2

Selanjutnya kita substitusikan nilai b = −1/2.

−1/2 = a² − 9/2
    a² = 9/2 − 1/2
         = 8/2 = 4
      a = ±2

Karena titik P berada pada kuadran III, maka nilai a adalah negatif.

a = −2

Dengan demikian, nilai dari

a + b = −2 + (−1/2)
         = −4/2 − 1/2
         = −5/2

Jadi, nilai a + b adalah −5/2 (B).

Simak Pembahasan Soal TKD Saintek SBMPTN 2018 selengkapnya.

No. 01 - 05 (Mat)	No. 31 - 35 (Kim)
No. 06 - 10 (Mat)	No. 36 - 40 (Kim)
No. 11 - 15 (Mat)	No. 41 - 45 (Kim)
No. 16 - 20 (Fis)	No. 46 - 50 (Bio)
No. 21 - 25 (Fis)	No. 51 - 55 (Bio)
No. 26 - 30 (Fis)	No. 56 - 60 (Bio)

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.