Soal FUNGSI Matematika SMA-IPA dan Pembahasan

Pembahasan soal Ujian Nasional (UN) Matematika SMA-IPA dengan materi pembahasan FUNGSI yang meliputi:

• fungsi, 
• daerah asal (domain) fungsi, dan 
• penerapan fungsi dalam kehidupan sehari-hari.

Soal No. 1 tentang Penerapan Fungsi

Dina harus membantu orang tuanya berjualan bahan makanan di toko keluarganya. Dina mendapat uang saku berdasarkan jumlah barang yang terjual pada hari tersebut dengan fungsi U(x) = 1.500x + 500, dengan U adalah uang saku dalam rupiah dan x adalah jumlah barang dalam unit. Jika jumlah barang yang terjual tergantung pada waktu yang dihabiskan Dina di toko keluarganya dengan x(t) = 2t + 3, di mana t adalah waktu dalam jam, maka besar uang saku Dina jika dia membantu selama 2 jam pada suatu hari adalah ….

A.	Rp10.500,00
B.	Rp11.000,00
C.	Rp11.500,00
D.	Rp12.000,00
E.	Rp12.500,00

UN 2018

Pembahasan

Selama 2 jam Dina dapat menjual barang sebanyak:

x(t)	=	2t + 3
x(2)	=	2 × 2 + 3
	=	4 + 3
	=	7

Dengan demikian, uang saku yang Dina terima adalah:

U(x)	=	1.500x + 500
U(7)	=	1.500 × 7 + 500
	=	10.500 + 500
	=	11.000

Jadi, besar uang saku yang diterima Dina adalah Rp11.000,00 (C).

Soal No. 2 tentang Penerapan Fungsi

Suatu pabrik kertas dengan bahan dasar kayu (x) memproduksi kertas melalui dua tahap. Tahap pertama menggunakan mesin I menghasilkan bahan kertas setengah jadi (m) dengan mengikuti m = f(x) = x² − 3x − 2. Tahap kedua menggunakan mesin II menghasilkan kertas mengikuti fungsi g(m) = 4m + 2, dengan x dan m dalam satuan ton. Jika bahan dasar kayu yang tersedia untuk produksi sebesar 4 ton, banyak kertas yang dihasilkan adalah ….

A.	5 ton
B.	10 ton
C.	15 ton
D.	20 ton
E.	30 ton

Pembahasan

Bahan setengah jadi yang dihasilkan oleh mesin I dengan bahan dasar kayu 4 ton adalah:

m	=	f(x) = x2 − 3x − 2
	=	f(4) = 42 − 3 × 4 − 2
	=	2

Selanjutnya bahan setengah jadi (m = 2) diolah oleh mesin II menjadi kertas.

g(m)	=	4m + 2
g(2)	=	4 × 2 + 2
	=	10

Jadi, banyak kertas yang dihasilkan adalah 10 ton (B).

Soal No. 3 tentang Fungsi

Diketahui f(x) = x + 3. Untuk x = 2, nilai dari f²(x) + 5f(x²) − 3f(x) adalah ….

A.	45
B.	35
C.	27
D.	24
E.	23

Pembahasan

Perhatikan perbedaan antara f²(x) dan f(x²)!

    f²(x) + 5f(x²) − 3f(x)
= (x + 3)² + 5(x² + 3) − 3(x + 3)

Tidak perlu diteruskan, langsung kita masukkan x = 2.

= (2 + 3)² + 5(2² + 3) − 3(2 + 3)
= 25 + 35 − 25
= 35

Jadi, nilai dari f²(x) + 5f(x²) − 3f(x) adalah 35 (B).

Soal No. 4 tentang Daerah Asal Fungsi

Agar fungsi

terdefinisi maka daerah asal f(x) adalah ….

A.	{x│x ≤ −4/3, x ≠ −2, x ∈ R}
B.	{x│x ≥ 4/3, x ∈ R}
C.	{x│x ≥ −2, x ∈ R}
D.	{x│−2 ≤ x ≤ 4/3, x ∈ R}
E.	{x│x ≤ −2 atau x ≥ 4/3, x ∈ R}

UN 2019

Pembahasan

Fungsi di atas adalah fungsi akar. Agar terdefinisi, fungsi tersebut harus memenuhi syarat akar: yang diakar harus lebih besar atau sama dengan nol.

Sementara itu, fungsi yang diakar berbentuk pecahan sehingga penyebutnya tidak boleh sama dengan nol.

x + 2 ≠ 0
     x  ≠ −2

Garis bilangan dari kedua syarat tersebut adalah:

Dengan demikian hasil penyelesaiannya adalah:

x ≥ 4/3

Jadi, daerah asal fungsi tersebut adalah opsi (B).

Soal No. 5 tentang Daerah Asal Fungsi

Daerah asal fungsi

agar terdefinisikan adalah ….

A.	{x│1 ≤ x ≤ 4, x ∈ R}
B.	{x│x ≤ −1 atau 3 ≤ x ≤ 4, x ∈ R}
C.	{x│x ≤ −3 atau 1 ≤ x ≤ 4, x ∈ R}
D.	{x│1 ≤ x ≤ 3 atau x > 4, x ∈ R}
E.	{x│−3 ≤ x ≤ 1 atau x > 4, x ∈ R}

Pembahasan

Domain atau daerah asal fungsi h(x) adalah semua nilai x yang memenuhi fungsi h(x). Fungsi h(x) adalah fungsi akar. Agar terdefinisikan, fungsi tersebut harus memenuhi syarat akar, yaitu fungsi diakar harus lebih besar atau sama dengan nol.

Garis bilangan pertidaksamaan di atas adalah:

Karena fungsi tersebut berbentuk pecahan maka penyebutnya tidak boleh sama dengan nol.

x − 4	≠	0
x	≠	4

Sehingga garis bilangan di atas menjadi:

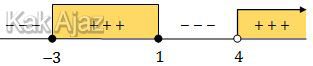
Dengan demikian hasil penyelesaiannya adalah:

−3 ≤ x ≤ 1 atau x > 4

Jadi, daerah asal fungsi tersebut adalah opsi (E).

Simak juga Pembahasan Matematika IPA UN: Komposisi dan Inves Fungsi.

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.