Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi

Pembahasan soal-soal Ujian Nasional SMA-IPA bidang studi Matematika dengan materi pembahasan Komposisi dan Invers Fungsi.

Soal tentang Komposisi dan Invers Fungsi UN 2012

Diketahui fungsi f(x) = 2x − 3 dan g(x) = x² + 2x − 3. Komposisi fungsi (g ∘ f)(x) = ....

A. 2x² + 4x − 9
B. 2x² + 4x − 3
C. 4x² + 6x − 18
D. 4x² + 8x
E. 4x² − 8x

Pembahasan

Komposisi fungsi (g ∘ f)(x) artinya fungsi f(x) tersarang dalam fungsi g(x) sehingga yang menjadi patokan adalah fungsi g(x).

        g(x) = x² + 2x − 3
(g ∘ f)(x) = f²(x) + 2f(x) − 3
               = (2x − 3)² + 2(2x − 3) − 3
               = 4x² − 12x + 9 + 4x − 6 − 3
               = 4x² − 8x

Jadi, komposisi fungsi tersebut adalah opsi (E).

Soal tentang Komposisi dan Invers Fungsi UN 2011

Diketahui f(x) = 2x + 5 dan
$g(x)=\frac{x-1}{x+4}, x\neq -4$
Hasil dari (f ∘ g)(x) = ....

$\textrm{A. }\; \; \frac{7x-2}{x+4}, x\neq -4$
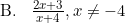
$\textrm{B. }\; \; \frac{2x+3}{x+4}, x\neq -4$
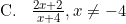
$\textrm{C. }\; \; \frac{2x+2}{x+4}, x\neq -4$
$\textrm{D. }\; \; \frac{7x+18}{x+4}, x\neq -4$
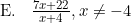
$\textrm{E. }\; \; \frac{7x+22}{x+4}, x\neq -4$

Pembahasan

Dengan berpedoman pada fungsi f(x) soal di atas dapat diselesaikan sebagai berikut:

         f(x) = 2x + 5
(f ∘ g)(x) = 2g(x) + 5
               $=2\left ( \frac{x-1}{x+4} \right )+5$
             $=\frac{2x-2}{x+4}+\frac{5x+20}{x+4}$
               $=\frac{7x+18}{x+4}$

Jadi, nilai dari komposisi fungsi tersebut adalah opsi (D).

Soal tentang Komposisi dan Invers Fungsi UN 2013

Diketahui fungsi

$g(x)=\frac{x+1}{2x-3},x\neq \frac{3}{2}$
Invers fungsi g adalah g⁻¹(x) = ....

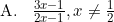
$\textrm{A. }\; \; \frac{3x-1}{2x-1},x\neq \frac{1}{2}$
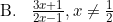
$\textrm{B. }\; \; \frac{3x+1}{2x-1},x\neq \frac{1}{2}$
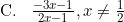
$\textrm{C. }\; \; \frac{-3x-1}{2x-1},x\neq \frac{1}{2}$
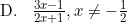
$\textrm{D. }\; \; \frac{3x-1}{2x+1},x\neq -\frac{1}{2}$
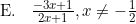
$\textrm{E. }\; \; \frac{-3x+1}{2x+1},x\neq -\frac{1}{2}$

Pembahasan

Invers fungsi bentuk tersebut dapat diselesaikan dengan rumus

$Rumus invers fungsi bentuk ax+b/cx+d$

Nilai a, b, c, dan d pada soal adalah

a = 1
b = 1
c = 2
d = −3

Nilai invers fungsi g(x) adalah

$g^{-1}(x)=\frac{{\color{DarkRed} -d}x+b}{cx{\color{DarkRed} -a}},x\neq \frac{a}{c}$
$=\frac{3x+1}{2x-1},x\neq \frac{1}{2}$

Jadi, invers fungsi g adalah opsi (B).

Soal tentang Komposisi dan Invers Fungsi UN 2010

Diketahui

$f(x)=\frac{9x+4}{6x-5},x\neq \frac{5}{6}$

dan fungsi invers f(x) adalah f⁻¹(x). Nilai f⁻¹(−2) = ....

A.   14/3
B.   17/14
C.   6/21
D.   −17/14
E. −14/3

Pembahasan

Dengan menggunakan rumus invers fungsi pada soal sebelumnya, diperoleh

$f^{-1}(x)=\frac{5x+4}{6x-9},x\neq \frac{3}{2}$
$f^{-1}(-2)=\frac{-10+4}{-12-9}$
= 6/21

Jadi, nilai untuk f⁻¹(−2) adalah 6/21 (C).

Soal tentang Komposisi dan Invers Fungsi UN 2014

Diketahui fungsi f : R → R dan g : R → R dirumuskan dengan f(x) = 2x − 1 dan
$g(x)=\frac{x+3}{2-x},x\neq 2.$
Fungsi invers dari (f ∘ g)(x) adalah (f ∘ g)⁻¹(x) = ....

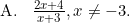
$\textrm{A. }\; \; \frac{2x+4}{x+3},x\neq -3.$
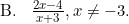
$\textrm{B. }\; \; \frac{2x-4}{x+3},x\neq -3.$
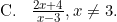
$\textrm{C. }\; \; \frac{2x+4}{x-3},x\neq 3.$
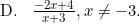
$\textrm{D. }\; \; \frac{-2x+4}{x+3},x\neq -3.$
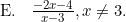
$\textrm{E. }\; \; \frac{-2x-4}{x-3},x\neq 3.$

Pembahasan

Kita tentukan (f ∘ g)(x) terlebih dahulu

        f(x) = 2x − 1
(f ∘ g)(x) = 2g(x) − 1
               $=2\left ( \frac{x+3}{2-x} \right )-1$
               $=\frac{2x+6}{2-x}-\frac{2-x}{2-x}$
               $=\frac{3x+4}{-x+2}$

Selanjutnya kita tentukan inversnya dengan menggunakan rumus invers di atas.

$(f\circ g)^{-1}(x)=\frac{-2x+4}{-x-3}$
                       $=\frac{-2x+4}{-x-3}\times \frac{-1}{-1}$
                       $=\frac{2x-4}{x+3},x\neq -3$

Jadi, invers dari komposisi fungsi tersebut adalah opsi (B).

Pembahasan soal Komposisi dan Invers Fungsi yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 11 dan 12
Pembahasan Matematika IPA UN 2014 No. 11
Pembahasan Matematika IPA UN 2015 No. 13
Pembahasan Matematika IPA UN 2016 No. 9 dan 10
Pembahasan Matematika IPA UN 2017 No. 6 dan 7
Pembahasan Matematika IPA UN 2018 No. 2
Pembahasan Matematika IPA UN 2019 No. 7 dan 8
Pembahasan Matematika IPA UN 2019 (2) No. 10
Pembahasan Matematika IPA UN 2019 (2) No. 11

Simak juga, Soal FUNGSI Matematika SMA-IPA dan Pembahasan,.

Dapatkan pembahasan soal dalam file pdf di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

7 comments:

Unknown20 March 2019 at 22:52
Kak,pembahasan nomor 1 bukannya bila (g o f) (x)= f(g(x))
Jadi jawabannya 2x^2 + 4x - 9 (a)
David Hake3 June 2020 at 20:24
sangat membantu sekali
David Hake3 June 2020 at 20:24
easy

Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.

Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan

Friday, 26 February 2016