Pembahasan Matematika IPA UN 2019 No. 21 - 25 Paket 2

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA Paket 2 nomor 21 sampai dengan nomor 25 tentang:

• integral substitusi, 
• trigonometri, 
• grafik fungsi trigonometri, 
• aturan sinus dan kosinus, serta 
• dimensi tiga [jarak titik ke garis].

Soal No. 21 tentang Integral Substitusi

Hasil dari ∫ (2x − 1) (x² − x + 3)³ dx = ⋯.

A.	⅓ (x2 − x + 3)3 + C
B.	¼ (x2 − x + 3)3 + C
C.	¼ (x2 − x + 3)4 + C
D.	½ (x2 − x + 3)4 + C
E.	(x2 − x + 3)4 + C

Pembahasan

Integral di atas termasuk integral substitusi. Cirinya, terdiri dari dua fungsi dengan derajat (pangkat tertinggi) berselisih satu.

Adapun cara penyelesaiannya sebagai berikut:

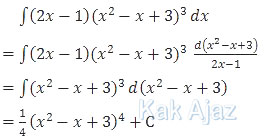
Jadi, hasil dari integral tersebut adalah (C).

Perdalam materi ini di Pembahasan Matematika UN: Integral Fungsi Aljabar.

Soal No. 22 tentang Trigonometri

Diketahui cos ⁡α = a/2b, dengan α sudut lancip. Nilai csc ⁡α = ⋯.

Pembahasan

Perhatikan gambar berikut ini!

Karena α sudut lancip (kuadran I) maka semua nilai trigonometri bernilai positif.

Jadi, nilai dari csc⁡α adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika UN: Perbandingan Trigonometri.

Soal No. 23 tentang Grafik Fungsi Trigonometri

Gambar grafik fungsi trigonometri f(x) = 2 sin⁡ (x − 30)° adalah ….

Pembahasan

Fungsi f(x) = 2 sin⁡ (x − 30)° sudah tampak jelas mempunyai amplitudo 2. [opsi C, D, dan E salah]

Sekarang kita tentukan pembuat nol-nya.

y	=	0
2 sin⁡ (x − 30)°	=	0
sin⁡ (x − 30)°	=	0
x − 30°	=	0°, 180°, 360°, …
x	=	30°, 210°, 390°, …

Grafik fungsi sinus dengan pembuat nol di atas adalah:

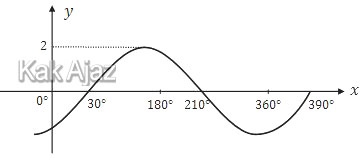
Jadi, grafik fungsi f(x) = 2 sin⁡ (x − 30)° adalah grafik pada opsi (A).

Perdalam materi ini di Fungsi Trigonometri dan Grafknya [Soal UN dan Pembahasan].

Soal No. 24 tentang Aturan Sinus dan Kosinus

Sebidang tanah berbentuk segitiga dengan setiap titik sudutnya diberi tonggak pembatas A, B, dan C. Jika jarak antara tonggak A dan B adalah 300 m, sudut ABC = 45°, dan sudut BCA = 60°, jarak antara tonggak A dan C adalah ….

A.	50√6 m
B.	100√3 m
C.	150√2 m
D.	100√6 m
E.	300√6 m

Pembahasan

Perhatikan gambar berikut ini!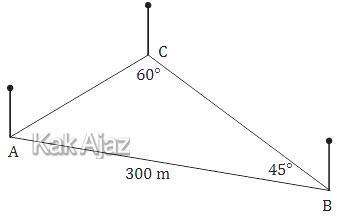

Karena diketahui dua sudut dan satu sisi, kita gunakan aturan sinus segitiga.

Jadi, jarak antara tonggak A dan C adalah 100√6 m (D).

Perdalam materi ini di Pembahasan Matematika UN: Aturan Sinus dan Kosinus.

Soal No. 25 tentang Dimensi Tiga [jarak titik ke garis]

Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P, Q, dan R berturut-turut merupakan titik tengah rusuk EH, BF, dan CG. Jarak titik P ke garis QR adalah ….

A.	3√7 cm
B.	3√6 cm
C.	3√5 cm
D.	3√3 cm
E.	2√3 cm

Pembahasan

Perhatikan gambar berikut ini!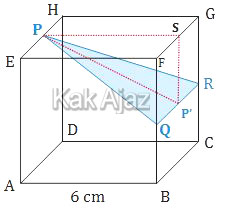

Jarak titik P ke garis QR, yaitu PP’ merupakan tinggi segitiga PQR. Selain itu, PP’ juga merupakan sisi miring segitiga siku-siku PP’S. Sehingga,

Jadi, jarak dari titik P ke garis QR adalah 3√5 cm (C).

Perdalam materi ini di Pembahasan Matematika UN: Dimensi Tiga.

Simak Pembahasan Soal Matematika IPA UN 2019 Paket 2 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.