
Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 Kode Naskah 157 nomor 1 sampai dengan nomor 5 tentang:
- sistem persamaan linear,
- matematika keuangan,
- pertidaksamaan,
- vektor, dan
- persamaan trigonometri.
Soal No. 1 tentang Sistem Persamaan Linear
Jika x dan y memenuhi
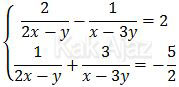
maka nilai x + 2y = ….
A. 1
B. 2
C. 3
D. 4
E. 5
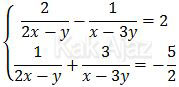
maka nilai x + 2y = ….
A. 1
B. 2
C. 3
D. 4
E. 5
Pembahasan
Karena kedua persamaan di atas mengandung penyebut yang sama maka dapat kita misalkan: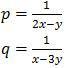
Sehingga diperoleh sistem persamaan linear:
2p − q = 2 … (1)
p + 3q = −5/2 … (2)
Selanjutnya kita eliminasi kedua persamaan tersebut dengan mengalikan 2 pada persamaan (2) terlebih dahulu. Diperoleh:
2p − q = 2
2p + 6q = −5
⎯⎯⎯⎯⎯⎯⎯⎯ −
−7q = 7
q = −1
Dengan diperolehnya q = −1, kita dapat memperoleh nilai p dari persamaan (1).
2p − q = 2
2p + 1 = 2
2p = 1
p = 1/2
Nah, sekarang perhatikan permisalan dan pertanyaan soal di atas!
Ternyata nilai x + 2y merupakan nilai dari 1/p − 1/q.
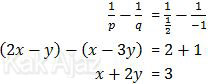
Jadi, nilai dari x + 2y adalah 3 (C).
Soal No. 2 tentang Matematika Keuangan
Seorang pelajar berencana untuk menabung di koperasi yang keuntungannya dihitung setiap semester. Apabila jumlah tabungan menjadi dua kali lipat dalam 5 tahun maka besar tingkat suku bunga per tahun adalah ….



Pembahasan
Soal di atas bisa saja diselesaikan dengan rumus bunga tunggal maupun bunga majemuk. Namun karena semua opsi jawaban mengandung operasi akar maka soal tersebut harus diselesaikan dengan rumus bunga majemuk.Adapun rumus bunga majemuk adalah sebagai berikut:
Mn = M0 (1 + i)n
dengan Mn : Modal setelah n periode
M0 : Modal awal
i : besar bunga
n : periode
Sementara itu, pada soal diketahui:
Mn = 2M0
n = 5 tahun
= 10 semester
Dengan demikian, rumus di atas menjadi:
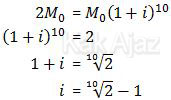
Tingkat suku bunga di atas adalah tingkat suku bunga per semester, sedangkan tingkat suku bunga per tahun adalah:
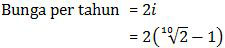
Jadi, besar tingkat suku bunga per tahun adalah opsi (A).
Soal No. 3 tentang Pertidaksamaan
Banyak bilangan bulat x yang memenuhi pertidaksamaan

adalah ….
A. 3
B. 4
C. 5
D. 6
E. 7

adalah ….
A. 3
B. 4
C. 5
D. 6
E. 7
Pembahasan
Langkah pertama menyelesaikan pertidaksamaan adalah memindahkan semua suku ke ruas kiri atau ruas kanan dijadikan nol.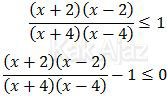
Selanjutnya kita selesaikan pertidaksamaan tersebut dengan menyamakan penyebutnya.
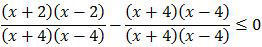
Kemudian pembilangnya kita jabarkan dengan menggunakan rumus (a + b)(a − b) = a2 − b2.

Nah, sekarang kita buat garis bilangan untuk bentuk pertidaksamaan terakhir ini.

Untuk menentukan daerah positif dan negatif, masukkan saja x = 1000 (hehehe... gak usah tanggung-tanggung). Hasilnya positif kan?
Sedangkan x = 1000 adalah daerah sebelah kanan. Berarti daerah sebelah kanan bernilai positif.
Selanjutnya daerah yang lain diisi secara berseling. Sehingga daerah tengah bernilai negatif dan daerah sebelah kiri bernilai negatif.
Berdasarkan garis bilangan di atas, hasil penentuan interval x adalah:
−4 ≤ x ≤ 4
Namun, perlu diingat! Pertidaksama di atas bertanda ‘≤’ (mengandung tanda ‘=’) sehingga harus diberlakukan syarat penyebut.
Penyebut suatu pecahan tidak boleh sama dengan nol sehingga:
x + 4 ≠ 0
x ≠ −4
x − 4 ≠ 0
x ≠ 4
Dengan memperhitungkan syarat penyebut di atas maka hasilnya penyelesaiannya adalah:
−4 < x < 4
Untuk x bilangan bulat, himpunan penyelesaian untuk x adalah:
x = {−3, −2, −1, 0, 1, 2, 3}
n(x) = 7
Jadi, banyak bilangan bulat x yang memenuhi pertidaksamaan tersebut adalah 7 (E).
Soal No. 4 tentang Vektor
Diketahui tiga vektor a, b, dan c dengan b ∙ c = 9 dan c = b + a. Misalkan γ adalah sudut antara vektor a dan c. Jika γ = 30° dan |c| = 6 maka |a| = ….
A. 1/4
B. 1/3
C. 1/3 √3
D. 1/4 √7
E. 3√3
A. 1/4
B. 1/3
C. 1/3 √3
D. 1/4 √7
E. 3√3
Pembahasan
Diketahui:b ∙ c = 9
c = b + a atau a = c − b
|c| = 6
γ = 30°
Karena γ adalah sudut antara vektor a dan c maka berlaku rumus:

Data untuk vektor a tidak diketahui sehingga kita perlu mengganti a menjadi a = c − b. Diperoleh:
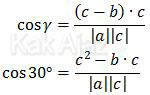
Pada vektor berlaku a2 = |a|2 sehingga diperoleh:

Jadi, nilai dari |a| adalah 3√3 (E).
Soal No. 5 tentang Persamaan Trigonometri
Jika
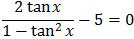
dengan 0 < x < π/2 maka cos2 x − sin2 x = ….
A. 1/√26
B. 2/√26
C. 3/√26
D. 4/√26
E. 5/√26
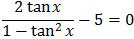
dengan 0 < x < π/2 maka cos2 x − sin2 x = ….
A. 1/√26
B. 2/√26
C. 3/√26
D. 4/√26
E. 5/√26
Pembahasan
Untuk menyelesaikan soal di atas, sebaiknya memahami kembali rumus trigonometri sudut ganda berikut ini: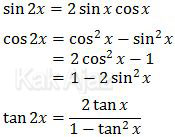
Dengan berpedoman pada rumus di atas, soal di atas dapat diselesaikan dengan mudah sebagai berikut:
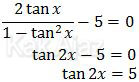
Sekarang kita buat segitiga trigonometri untuk tan 2x = 5.

Dengan demikian,
cos2 x − sin2 x = cos 2x
= 1/√26
Jadi, nilai dari cos2 x − sin2 x adalah 1/√26 (A).
Simak Pembahasan Soal TKD Saintek SBMPTN 2017 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan