- penarikan kesimpulan,
- ekuivalensi,
- perpangkatan,
- bentuk akar, dan
- logaritma.
Soal No. 1 tentang Penarikan Kesimpulan
Diketahui premis-premis berikut:
A. Saya tidak bermain dan saya gagal dalam ujian.
B. Jika saya bermain maka saya tidak gagal dalam ujian.
C. Saya bermain.
D. Saya belajar.
E. Saya tidak bermain.
- Saya bermain atau saya tidak gagal dalam ujian.
- Saya gagal dalam ujian.
A. Saya tidak bermain dan saya gagal dalam ujian.
B. Jika saya bermain maka saya tidak gagal dalam ujian.
C. Saya bermain.
D. Saya belajar.
E. Saya tidak bermain.
Pembahasan
Mengerjakan soal logika matematika tidak boleh menggunakan perasaan atau penalaran di luar kepala, tetapi harus dianalisis secara matematis. Ok, kita misalkan terlebih dahulu bagian-bagian dari kedua premis tersebut.p : Saya bermain.
q : Saya gagal dalam ujian.
Sekarang kita analisis masing-masing premis.
Premis 1 :
Saya bermain atau saya tidak gagal dalam ujian.
≡ p ∨ ~q
Premis 2 :
Saya gagal dalam ujian.
≡ q
Premis 1 berbentuk disjungsi. Agar bisa ditarik kesimpulan, bentuknya harus diubah menjadi implikasi. Kesetaraan antara disjungsi dan implikasi adalah
p ∨ q ≡ ~p ⇒ q
Berdasarkan kesetaraan di atas, diperoleh
p ∨ ~q ≡ ~p ⇒ ~q
Setelah premis 1 sudah dalam bentuk implikasi, kita dapat menarik kesimpulan dari premis 1 dan 2 dengan menggunakan modus Tollens.
~p ⇒ ~q
q
⎯⎯⎯⎯⎯⎯
∴ p (Saya bermain)
Jadi, kesimpulan yang sah dari dua premis tersebut adalah 'Saya bermain' (C).
Soal No. 2 tentang Ekuivalensi
Pernyataan yang setara dengan pernyataan "Jika semua siswa kelas XII Ujian Nasional maka semua siswa kelas X dan XI belajar di rumah" adalah ...
A. Semua siswa kelas X dan XI belajar di rumah dan siswa kelas XII Ujian Nasional.
B. Beberapa siswa kelas XII Ujian Nasional atau beberapa siswa kelas X dan XI belajar di rumah.
C. Beberapa siswa kelas XII tidak Ujian Nasional atau semua siswa kelas X dan XI belajar di rumah.
D. Semua siswa kelas XII Ujian Nasional dan beberapa siswa kelas X dan XI belajar di rumah.
E. Beberapa siswa kelas XII tidak Ujian Nasional atau beberapa siswa kelas X dan XI belajar di rumah.
A. Semua siswa kelas X dan XI belajar di rumah dan siswa kelas XII Ujian Nasional.
B. Beberapa siswa kelas XII Ujian Nasional atau beberapa siswa kelas X dan XI belajar di rumah.
C. Beberapa siswa kelas XII tidak Ujian Nasional atau semua siswa kelas X dan XI belajar di rumah.
D. Semua siswa kelas XII Ujian Nasional dan beberapa siswa kelas X dan XI belajar di rumah.
E. Beberapa siswa kelas XII tidak Ujian Nasional atau beberapa siswa kelas X dan XI belajar di rumah.

Pembahasan
Misal:p : Siswa kelas XII Ujian Nasional.
q : Siswa kelas X dan XI belajar di rumah.
Pernyataan "Jika semua siswa kelas XII Ujian Nasional maka semua siswa kelas X dan XI belajar di rumah" dapat dinotasikan menjadi
∀p ⇒ ∀q
Pernyataan yang setara atau ekuivalen dengan implikasi tersebut adalah
∀p ⇒ ∀q ≡ ∃~q ⇒ ∃~p (kontraposisi)
∀p ⇒ ∀q ≡ ∃~p ∨ ∀q (negasi dua kali)
Berdasarkan ekuivalensi tersebut, pernyataan yang setara dengan pernyataan di atas adalah
- Jika beberapa siswa kelas X dan XI tidak belajar di rumah maka beberapa siswa kelas XII tidak Ujian Nasional.
- Beberapa siswa kelas XII tidak Ujian Nasional atau semua siswa kelas X dan XI belajar di rumah.
Soal No. 3 tentang Perpangkatan
Bentuk sederhana dari
%5E%7B2%7D)
adalah ....
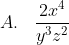
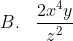
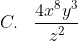
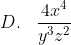
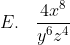
adalah ....
Pembahasan
Langkah pertama adalah mengubah pangkat negatif menjadi pangkat positif. Cara dengan mengubah letak, bila bilangan yang berpangkat negatif letaknya pada posisi pembilang maka dengan mengubah letak ke posisi penyebut pangkatnya akan menjadi positif. Demikian juga sebaliknya. Langkah berikutnya tinggal menjumlah pangkat masing-masing.Jadi, bentuk sederhana dari perpangkatan tersebut adalah opsi (E).
Untuk memperdalam, silakan pelajari Pembahasan Soal UN: Perpangkatan.
Soal No. 4 tentang Bentuk Akar
Bentuk sederhana dari
%5Cleft&space;(&space;%5Csqrt%7B5%7D-%5Csqrt%7B3%7D&space;%5Cright&space;)%7D%7B%5Csqrt%7B3%7D+2%7D)
adalah ....
A. 4 − 2√3
B. 2 − √3
C. −2 + √3
D. −4 + √3
E. −4 − 2√3
adalah ....
A. 4 − 2√3
B. 2 − √3
C. −2 + √3
D. −4 + √3
E. −4 − 2√3
Pembahasan
Perhatikan pembilangnya! Pembilangnya berbentuk (a + b) (a − b) sehingga dapat disederhanakan menjadi(a + b)(a − b) = a2 − b2
(√5 + √3)(√5 − √3) = 5 − 3
= 2
Untuk sementara bentuk sederhana dari bentuk akar tersebut adalah
Bentuk ini dapat disederhanakan lagi dengan cara mengalikan bilangan sekawan dari penyebutnya.
= −2√3 + 4
= 4 − 2√3
Jadi, bentuk sederhana dari bentuk akar tersebut adalah 4 − 2√3 (A).
Perdalam materi ini di Pembahasan Soal UN: Bentuk Akar.
Soal No. 5 tentang Logaritma
Hasil dari
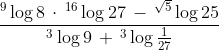
adalah ....
A. 25/8
B. 23/8
C. 7/4
D. −7/4
E. −23/8
adalah ....
A. 25/8
B. 23/8
C. 7/4
D. −7/4
E. −23/8
Pembahasan
Kita ubah dulu angka-angka pada soal di atas menjadi bilangan berpangkat.Kita gunakan rumus anlog bm = m/n alog b untuk menyederhanakan bentuk di atas.
Mengingat alog b . blog a = 1 dan alog a = 1 maka diperoleh
= 23/8
Jadi, hasil dari bentuk logaritma tersebut adalah 23/8 (B).
Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan