Pembahasan Matematika IPA UN 2015 No. 26 - 30.

Pembahasan soal Matematika IPA Ujian Nasional 2015 nomor 26 sampai dengan nomor 30 tentang:

• aturan sinus dan kosinus, 
• persamaan trigonometri, 
• rumus jumlah dan selisih dua sudut, 
• limit fungsi aljabar, serta 
• limit fungsi trigonometri.

Soal No. 26 tentang Aturan Sinus dan Kosinus

Perhatikan gambar!

Panjang AD adalah ....

A.   3√7 cm
B.   4√7 cm
C.   2√17 cm
D.   2√19 cm
E.   4√17 cm 

Pembahasan

Perhatikan segitiga ABC!

Pada segitiga tersebut diketahui dua sudut dan satu sisi sehingga berlaku aturan sinus.


 
   AC = 12

Sekarang perhatikan segitiga ACD!

Karena panjang AC sudah kita tentukan maka pada segitiga tersebut mempunyai dua sisi dan satu sudut yang diketahui sehingga berlaku aturan kosinus. 

    c² = a² + d² − 2 a d cos C
AD² = 4² + 12² − 2 . 4 . 12 cos 60°
        = 16 + 144 − 96 . 0,5
        = 112
AD  = 4√7

Jadi, panjang AD pada gambar tersebut adalah 4√7 cm (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus.

Soal No. 27 tentang Persamaan Trigonometri

Himpunan penyelesaian persamaan cos 2x + 3 cos x − 1 = 0 pada 0° ≤ x ≤ 360° adalah ....

A.   {60°, 120°}
B.   {60°, 240°}
C.   {60°, 300°}
D.   {120°, 240°}
E.   {120°, 300°}

Pembahasan

Persamaan tersebut harus diubah menjadi satu variabel terlebih dahulu. Bentuk cos 2x diubah ke dalam bentuk cos x.

cos 2x = 2 cos² x − 1

Dengan demikian persamaan tersebut menjadi

2 cos² x − 1 + 3 cos x − 1 = 0
      2 cos² x + 3 cos x − 2 = 0
    (2 cos x − 1)(cos x + 2) = 0
cos x = ½  atau  cos x = −2

Penyelesaiannya adalah sebagai berikut:

cos x = ½
nilai cos x positif berada pada kuadran I dan IV
kuadran I   : cos x = cos 60° 
                          x = 60°
kuadran IV : cos x = cos (360° − 60°) 
                          x = 300°

cos x = −2
tidak memenuhi karena nilai cos x terletak pada interval −1 < cos x < 1.

Jadi, himpunan penyelesaian persamaan trigonometri tersebut adalah {60°, 300°} atau opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Trigonometri.

Soal No. 28 tentang Rumus Jumlah dan Selisih Dua Sudut

Diketahui cos (A + B) = 3/5 dan cos A . cos B = 2/3, A dan B sudut lancip. Nilai tan A . tan B adalah ....

A.   −3/10
B.   −1/5
C.   −2/15
D.   1/10
E.   3/10

Pembahasan

Kita gunakan rumus jumlah dua sudut pada kosinus.

cos (A + B) = cos A . cos B − sin A . sin B
             3/5 = 2/3 − sin A . sin B
sin A . sin B = 2/3 − 3/5
                   = 1/15

Tangen adalah perbandingan nilai sinus dan kosinus, diperoleh


                       

Jadi, nilai tan A . tan B adalah 1/10 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Perbandingan Trigonometri.

Soal No. 29 tentang Limit Fungsi Aljabar

Nilai dari



adalah ....

A.   −4
B.   −3
C.   −2
D.   0
E.   1 

Pembahasan

Bentuk umum limit di atas adalah




Mari kita ubah limit tersebut ke bentuk umumnya.

    



Berdasarkan bentuk umum di atas, kita peroleh: 

a = 9 
b = −6 
d = 6

Dengan demikian, hasil dari limit tersebut adalah



Jadi, nilai dari limit fungsi aljabar tersebut adalah −2 (C).

Soal No. 30 tentang Limit Fungsi Trigonometri

Nilai dari



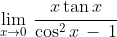
adalah ....

A.   1
B.   0
C.   −½
D.   −1
E.   −2

Pembahasan

Prinsip limit trigonometri dengan x → 0 adalah 

x = sin x = tan x

Berpegangan pada prinsip tersebut, bentuk kosinus harus diubah ke dalam bentuk sinus atau tangen.

cos² x + sin² x = 1
cos² x − 1 = −sin² x

Sehingga limit tersebut akan menjadi



Substitusi tan x = x dan sin x = x diperoleh



Jadi, nilai dari limit fungsi trigonometri tersebut adalah −1 (A D).

Thanks to rohmanjunior

Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi.

Simak Pembahasan Soal Matematika IPA UN 2015 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.