- lingkaran,
- trigonometri,
- vektor,
- transformasi geometri, dan
- dimensi tiga.
Soal No. 1 tentang Lingkaran
Misalkan titik A dan B pada lingkaran
x2 + y2 − 6x − 2y + k = 0
sehingga garis singgung lingkaran di titik A dan B berpotongan di C(8, 1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12 maka k = ….
A. −1
B. 0
C. 1
D. 2
E. 3
x2 + y2 − 6x − 2y + k = 0
sehingga garis singgung lingkaran di titik A dan B berpotongan di C(8, 1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12 maka k = ….
A. −1
B. 0
C. 1
D. 2
E. 3
Pembahasan
Bentuk umum persamaan lingkaranx2 + y2 − 6x − 2y + k = 0 adalah x2 + y2 + Ax + By + C = 0.Berdasarkan bentuk umum ini diperoleh:A = −6
B = −2
C = k
pusat lingkaran: (−½A, −½B)
(−½×(−6), −½×(−2))
(3, 1)
Gambar ilustrasi untuk soal di atas adalah:
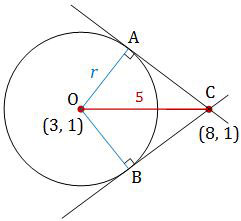
Luas segiempat OACB = 12 sehingga luas segitiga AOC = 6. Sedangkan segitiga AOC adalah segitiga siku-siku dengan panjang sisi miring = 5. Dengan demikian dapat dipastikan panjang sisi OA = 3 dan sisi AC = 4 (triple Pythagoras).
Nah, kita sudah mendapatkan nilai jari-jari lingkaran tersebut, yaitu r = OA = 3. Sekarang kita gunakan rumus jari-jari lingkaran untuk mendapatkan nilai k.

Jadi, nilai k pada persamaan lingkaran tersebut adalah 1 (C).
Soal No. 2 tentang Trigonometri
Jika tan(2x + 45°) = a dan tan(x + 30°) = b, ab ∉ {1, −1, √2, −√2}
maka tan(3x + 75°) tan(x + 15°) = ….

maka tan(3x + 75°) tan(x + 15°) = ….


Pembahasan
Kita buat permisalan dulu agar tampak lebih sederhana.Misal: A = 2x + 45° → tan A = a
B = x + 30° → tan B = b
Sehingga: A + B = 3x + 75°
A − B = x + 15°
Sekarang kita masuk ke bagian pertanyaan:
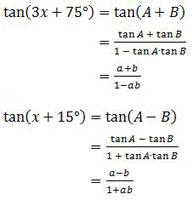
Dengan demikian, dengan menggunakan rumus (a + b)(a − b) = a2 − b2, diperoleh:
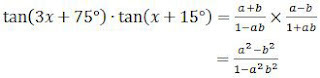
Jadi, nilai tan(3x + 75°) tan(x + 15°) adalah opsi (C).
Soal No. 3 tentang Vektor
Misalkan A(t2 + 1, t) dan B(1, 2) sehingga panjang vektor proyeksi OA terhadap OB kurang dari 4/√5, maka nilai t yang mungkin adalah ….
A. t < −1 atau t > 3
B. t < −3 atau t > 1
C. −3 < t < 1
D. −1 < t < 3
E. 1 < t < 3
A. t < −1 atau t > 3
B. t < −3 atau t > 1
C. −3 < t < 1
D. −1 < t < 3
E. 1 < t < 3
Pembahasan
Panjang vektor proyeksi OA terhadap OB kurang dari 4/√5:
t2 + 2t + 1 < 4
t2 + 2t − 3 < 0
(t + 3)(t − 1) < 0
Karena koefisien t2 positif maka tanda pertidaksamaan "<" mempunyai daerah penyelesaian di antara t = −3 dan t = 1. Diperoleh:
−3 < t < 1
Jadi, nilai t yang mungkin adalah −3 < t < 1 (C).
Soal No. 4 tentang Transformasi Geometri
Pencerminan garis y = −x + 2 terhadap garis y = 3 menghasilkan garis ….
A. y = x + 4
B. y = −x + 4
C. y = x + 2
D. y = x − 2
E. y = −x − 4
A. y = x + 4
B. y = −x + 4
C. y = x + 2
D. y = x − 2
E. y = −x − 4
Pembahasan
Pencerminan terhadap garis y = k dirumuskan sebagai:P(x, y) —→ P'(x, 2k − y)
Sehingga diperoleh:
x' = x
y' = 2k − y (k = 3)
= 2×3 − y
= 6 − y
Dengan demikian, hasil pencerminan garis y = −x + 2 adalah:
y' = −x' + 2
6 − y = −x + 2
−y = −x − 4
y = x + 4
Jadi, pencerminan garis y = −x + 2 terhadap garis y = 3 menghasilkan garis y = x + 4 (A).
Soal No. 5 tentang Dimensi Tiga
Pada kubus ABCD.EFGH, P adalah pad EH dengan EP : PH = 1 : 2 dan titik Q pada GH dengan GQ : QH = 1 : 2. Perpanjangan AP dan CQ berpotongan di perpanjangan DH di titik R.

Jika panjang rusuk kubus adalah 6 maka volume ACD.PQH adalah ….
A. 46
B. 52
C. 54
D. 76
E. 81

Jika panjang rusuk kubus adalah 6 maka volume ACD.PQH adalah ….
A. 46
B. 52
C. 54
D. 76
E. 81
Pembahasan
Perhatikan segitiga DCR!
Segitiga CDR sebangun dengan segitiga HQR sehingga diperoleh perbandingan:

6x = 24 + 4x
2x = 24
x = 12
Volume bangun ACD.PQH merupakan pengurangan dari volume limas R.ACD dengan limas R.PQH. Mari kita tentukan volume masing-masing limas tersebut!
Volume limas R.ACD (V1)
V1 = ⅓ × La × t
= ⅓ × L ΔACD × DR
= ⅓ × ½ . 6 . 6 × 18
= 108
Volume limas R.PQH (V2)
V2 = ⅓ × La × t
= ⅓ × L ΔPQH × HR
= ⅓ × ½ . 4 . 4 × 12
= 32
Dengan demikian, volume ACD.PQH adalah:
V = V1 − V2
= 108 − 32
= 76
Jadi, volume bangun ruang ACD.PQH adalah 76 satuan volume (D).
Simak Pembahasan Soal TKD Saintek SBMPTN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan