- suku banyak,
- pertidaksamaan eksponen,
- persamaan eksponen dan logaritma,
- limit fungsi, serta
- barisan dan deret.
Soal No. 6 tentang Suku Banyak
Sisa pembagian
A(x − 2)2014 + (x − 1)2015 − (x − 2)2
oleh x2 − 3x + 2 adalah Bx − 1. Nilai 5A + 3B adalah ….
A. 0
B. 2
C. 4
D. 6
E. 8
A(x − 2)2014 + (x − 1)2015 − (x − 2)2
oleh x2 − 3x + 2 adalah Bx − 1. Nilai 5A + 3B adalah ….
A. 0
B. 2
C. 4
D. 6
E. 8
Pembahasan
Pembagi suku banyak tersebut adalah x2 − 3x + 2 yang dapat difaktorkan menjadi (x − 2)(x − 1). Artinya:Jika f(x) dibagi x2 − 3x + 2 sisa s(x) = Bx − 1
maka f(x) dibagi x − 2 sisa s(2) = 2B − 1
f(x) dibagi x − 1 sisa s(1) = B − 1
Misalkan suku banyak tersebut adalah f(x).
f(x) = A(x − 2)2014 + (x − 1)2015 − (x − 2)2
Menurut teorema sisa, jika suku banyak f(x) dibagi x − a maka sisanya adalah f(a). Sehingga:
f(x) dibagi x − 2
sisa = f(2)
s(2) = f(2)
2B − 1 = A(2 − 2)2014 + (2 − 1)2015 − (2 − 2)2
= 0 + 1 − 0
= 1
2B = 2
B = 1
f(x) dibagi x − 1
sisa = f(1)
s(1) = f(1)
B − 1 = A(1 − 2)2014 + (1 − 1)2015 − (1 − 2)2
1 − 1 = A + 0 − 1
0 = A − 1
A = 1
Dengan demikian:
5A + 3B = 5×1 + 3×1
= 5 + 3
= 8
Jadi, nilai 5A + 3B adalah 8 (E).
Soal No. 7 tentang Pertidaksamaan Eksponen
Nilai c yang memenuhi
(0,25)(3x2 − 2x − 4) < (0,0625)(x2 + x − c)
adalah ….
A. −4 < c < 0
B. 0 < c < 4
C. c < −4
D. c < 4
E. c > 4
(0,25)(3x2 − 2x − 4) < (0,0625)(x2 + x − c)
adalah ….
A. −4 < c < 0
B. 0 < c < 4
C. c < −4
D. c < 4
E. c > 4

Pembahasan
Langkah pertama untuk menyelesaikan soal di atas adalah menyamakan bilangan pokoknya, yaitu 0,0625 dijadikan (0,25)2. Diperoleh:(0,25)(3x2 − 2x − 4) < (0,0625)(x2 + x − c)
(0,25)(3x2 − 2x − 4) < (0,25)2(x2 + x − c)
Selanjutnya, untuk bilangan pokok 0 < a < 1, berlaku:
af(x) < ag(x) ⇔ f(x) > g(x)
(perhatikan, tanda pertidaksamaan dibalik)
Sehingga diperoleh:
3x2 − 2x − 4 > 2x2 + 2x − 2c
x2 − 4x − 4 + 2c > 0
Pertidaksamaan terakhir ini berarti persamaan kuadrat x2 − 4x − 4 + 2c bernilai positif atau definit positif. Syarat definit positif adalah diskriminan persamaan kuadrat tersebut kurang dari nol.
D < 0
b2 − 4aC < 0
(−4)2 − 4.1.(−4 + 2c) < 0
16 + 16 − 8c < 0
−8c < −32
c > 4
Jadi, nilai c yang memenuhi adalah c > 4 (E).
Soal No. 8 tentang Persamaan Eksponen dan Logaritma
Jika x1, x2 adalah akar-akar
252x − 52x+1 − 2 ∙ 52x+3 + a = 0
di mana x1 + x2 = 2 ∙ 5log 2 maka a = ….
A. 8
B. 8√2
C. 16
D. 16√2
E. 32
252x − 52x+1 − 2 ∙ 52x+3 + a = 0
di mana x1 + x2 = 2 ∙ 5log 2 maka a = ….
A. 8
B. 8√2
C. 16
D. 16√2
E. 32
Pembahasan
Bentuk eksponen kita pecah dengan menggunakan rumus am+n = am . an. Diperoleh:252x − 52x+1 − 2 ∙ 52x+3 + a = 0
252x − 52x . 51 − 2 ∙ 52x . 53 + a = 0
252x − 5 . 25x − 250 ∙ 25x + a = 0
252x − 255 . 25x + a = 0
Persamaan eksponen terakhir berbentuk persamaan kuadrat. Kita buat permisalan agar lebih tampak sederhana.
25x = p
252x = p2
Sehingga persamaan eksponen tersebut menjadi:
p2 − 255p + a = 0
Jika p1 dan p2 adalah akar persamaan tersebut maka perkalian akarnya adalah:
p1 . p2 = a
25x1 . 25x2 = a
25x1+x2 = a
Sedangkan pada soal diketahui bahwa:
x1 + x2 = 2 ∙ 5log 2
= 5log 22
= 5log 4
Sehingga diperoleh:
25x1+x2 = a
255log 4 = a
525log 4 = a
55log 16 = a
16 = a (mmlog x = x)
Jadi, nilai a adalah 16 (C).
Soal No. 9 tentang Limit Fungsi
Nilai dari
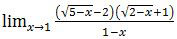
adalah ....
A. −1/2
B. −1/4
C. 1/8
D. 1/4
E. 1/2
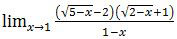
adalah ....
A. −1/2
B. −1/4
C. 1/8
D. 1/4
E. 1/2
Pembahasan
Limit bentuk di atas harus kita kalikan bilangan sekawan dari √(5 − x) − 2 karena bentuk akar ini akan menghasilkan nol bila disubstitusi x = 1.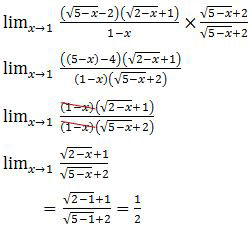
Jadi, nilai dari limit pada soal di atas adalah 1/2 (E).
Soal No. 10 tentang Barisan dan Deret
Jika u1, u2, u3, … adalah barisan geometri yang memenuhi u3 − u6 = x dan u2 − u4 = y maka x/y = ….


Pembahasan
Suku ke-n deret geometri memenuhi rumus:un = arn−1
Berdasarkan rumus tersebut, kita tentukan nilai untuk x dan y.
x = u3 − u6
= ar2 − ar5
= ar2(1 − r3)
y = u2 − u4
= ar − ar3
= ar(1 − r2)
Nah, sekarang tinggal kita bandingkan nilai x dan y.

Jadi, nilai perbandingan antara x dan y adalah opsi (C).
Simak Pembahasan Soal TKD Saintek SBMPTN 2015 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

halo, terimakasih ya kak sudah membantu kami dalam belajar dengan memberikan referensi soal-soal semoga sehat dan sukses selalu ya kakk!!
ReplyDeleteAmin
DeleteTerima kasih kembali, Adelia. Semogat semakin semangat belajar
Sangat membantu sekalii,,,terma kasih banyak kak
ReplyDeleteTerima kasih kembali
Delete