Pembahasan Matematika IPA UN: Perbandingan Trigonometri

Pembahasan soal-soal Ujian Nasional (UN) bidang studi Matematika SMA-IPA dengan materi pembahasan Perbandingan Trigonometri yang meliputi rumus jumlah dan selisih dua sudut serta rumus jumlah dan selisih sinus dan kosinus.

Untuk menyelesaikan soal-soal perbandingan trigonometri berikut ini, wajib hukumnya menghafal rumus jumlah dan selisih dua sudut serta rumus jumlah dan selisih sinus dan kosinus.

Rumus Jumlah dan Selisih Dua Sudut

sin⁡ (A + B) = sin ⁡A cos ⁡B + cos ⁡A sin ⁡B
sin⁡ (A − B) = sin ⁡A cos⁡ B − cos ⁡A sin ⁡B
cos⁡ (A + B) = cos ⁡A cos ⁡B − sin⁡ A sin ⁡B
cos (A − B) = cos ⁡A cos ⁡B + sin⁡ A sin ⁡B

Rumus Jumlah dan Selisih Sinus dan Kosinus

cos⁡ A + cos ⁡B = 2 cos⁡ ½(A + B) cos⁡ ½(A − B)
cos⁡ A − cos ⁡B = −2 sin ½(A + B) sin ½(A − B)
sin⁡ A + sin⁡ B = 2 sin ½(A + B) cos ½(A − B)
sin ⁡A − sin ⁡B = 2 cos⁡ ½(A + B) sin⁡ ½(A − B)

Soal tentang Perbandingan Trigonometri UN 2011

Diketahui A + B = ½π dan sin⁡ A sin⁡ B = ¼.
Nilai dari cos⁡ (A − B) adalah ….

A.   −1
B.   −½
C.   ½
D.   ¾
E.   1

Pembahasan

Modal untuk mengerjakan soal di atas adalah rumus jumlah dan selisih dua sudut pada fungsi kosinus:

cos⁡ (A ± B) = cos ⁡A cos ⁡B ∓ sin⁡ A sin ⁡B

Perhatikan tanda plus dan minus ruas kiri dan ruas kanan berbeda.

Pertama kita gunakan rumus jumlah dua sudut karena pada soal diketahui penjumlahan dua sudut, yaitu A + B = ½π = 90°.

cos⁡ (A + B) = cos ⁡A cos ⁡B − sin⁡ A sin ⁡B
       cos⁡ 90° = cos⁡ A cos⁡ B − ¼
                 0 = cos⁡A cos⁡B − ¼
  cos⁡A cos⁡B = ¼

Selanjutnya kita gunakan rumus selisih dua sudut sesuai dengan pertanyaan.

cos (A − B) = cos ⁡A cos ⁡B + sin⁡ A sin ⁡B
                   = ¼ + ¼
                   = ½

Jadi, nilai dari cos⁡ (A − B) adalah ½ (C).

Soal tentang Perbandingan Trigonometri UN 2015

Diketahui cos⁡ (A + B) = 1/5 dan cos ⁡A ∙ cos ⁡B = 2/3. A dan B sudut lancip. Nilai tan ⁡A ∙ tan⁡B adalah ….

A.   5/7
B.   7/10
C.   7/15
D.   −7/15
E.   −1/2

Pembahasan

Kita gunakan rumus jumlah dua sudut kosinus sesuai dengan data yang diketahui pada soal.

cos⁡ (A + B) = cos ⁡A cos ⁡B − sin⁡ A . sin ⁡B
             1/5 = 2/3 − sin ⁡A ∙ sin ⁡B
sin⁡ A ∙ sin⁡ B = 2/3 − 1/5
                   = 10/15 − 3/15
                   = 7/15

Tangens adalah perbandingan sinus dan kosinus, sehingga:

Jadi, nilai tan⁡ A ∙ tan⁡ B adalah 7/10 (B).

Soal tentang Perbandingan Trigonometri UN 2012

Nilai dari sin⁡ 75° − sin⁡ 165° adalah ….

A.   ¼√2
B.   ¼√3
C.   ¼√6
D.   ½√2
E.   ½√6

Pembahasan

Untuk soal di atas, kita gunakan rumus selisih sinus berikut ini:

sin ⁡A − sin ⁡B = 2 cos⁡ ½(A + B) sin⁡ ½(A − B)

Sesuai dengan rumus di atas maka:

   sin⁡ 75° − sin⁡ 165°
= 2 cos⁡ ½(75° + 165°) sin⁡ ½(75° − 165°)
= 2 cos 120° sin ⁡(−45°)

Sudut 120° masuk wilayah kuadran II sehingga bisa diganti 180° − 60°. Sedangkan sudut (−45°) masuk kuadran IV.

Perhatikan nilai trigonometri pada kuadran II dan IV berikut ini:

Kuadran II
sin⁡(180° − α)  = sin⁡α
cos⁡(180° − α) = −cos ⁡α
tan⁡(180° − α)  = −tan ⁡α

Kuadran IV
sin⁡ (−α)  = −sin ⁡α
cos ⁡(−α) = cos ⁡α
tan ⁡(−α)  = −tan ⁡α

Berdasarkan rumus di atas, diperoleh:

= 2 cos⁡ (180° − 60°) (−sin⁡ 45°)
= 2(−cos 60°)(−sin 45°)
= 2 cos⁡ 60° sin⁡ 45°
= 2 × ½ × ½√2
= ½√2

Jadi, Nilai dari sin⁡ 75° − sin⁡ 165° adalah ½√2 (D).

Soal tentang Perbandingan Trigonometri UN 2014

Nilai dari sin⁡ 75° − sin⁡ 15° + cos 45° = ….

A.   √3
B.   √2
C.   ½√2
D.   ⅓√2
E.   1

Pembahasan

Yang perlu diperhatikan pada soal di atas adalah sudut 75° dan sudut 15°. Kita gunakan rumus selisih sinus seperti soal sebelumnya.

   sin⁡ 75° − sin⁡ 15° + cos 45°
= 2 cos⁡ ½(75°+15°) sin⁡ ½(75° − 15°) + cos⁡ 45°
= 2 cos⁡ 45° sin⁡ 30° + cos⁡ 45°

Nah, sekarang semua sudutnya sudah termasuk sudut istimewa. Tinggal kiat selesaikan.

= 2 × ½√2 × ½ + ½√2
= ½√2 + ½√2
= √2

Jadi, nilai dari sin⁡ 75° − sin⁡ 15° + cos 45° adalah √2 (B).

Soal tentang Perbandingan Trigonometri UN 2013

Nilai dari

adalah ...

A.   −√3
B.   −1
C.   −⅓√3
D.   ⅓√3
E.   √3

Pembahasan

Perhatikan rumus penjumlahan sinus dan kosinus berikut ini!

cos⁡ A + cos ⁡B = 2 cos⁡ ½(A + B) cos⁡ ½(A − B)
sin⁡ A + sin⁡ B = 2 sin ½(A + B) cos ½(A − B)

Berdasarkan kedua rumus di atas, perbandingan antara penjumlahan kosinus dan sinus adalah:

Dengan demikian:

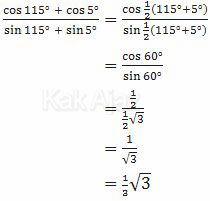
Jadi, nilai dari perbandingan trigonometri tersebut adalah  ⅓√3 (D).

Pembahasan soal Perbandingan Trigonometri yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 27
Pembahasan Matematika IPA UN 2014 No. 26
Pembahasan Matematika IPA UN 2015 No. 28
Pembahasan Matematika IPA UN 2016 No. 20
Pembahasan Matematika IPA UN 2017 No. 27 dan 28
Pembahasan Matematika IPA UN 2019 No. 24
Pembahasan Matematika IPA UN 2019 (2) No. 22

Simak juga,
Pembahasan Matematika IPA UN: Persamaan Trigonometri
Fungsi Trigonometri dan Grafiknya [Soal UN dan Pembahasan]
Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.