Pembahasan Matematika IPA UN 2017 No. 31 - 35

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 31 sampai dengan nomor 35 tentang:

• jarak titik ke garis pada dimensi tiga, 
• sudut antara garis dan bidang pada dimensi tiga, 
• transformasi geometri, 
• persamaan lingkaran, serta 
• garis singgung lingkaran.

Soal No. 31 tentang Jarak Titik ke Garis pada Dimensi Tiga

Diketahui limas beraturan T.ABCD dengan panjang rusuk tegak 6√2 cm dan panjang rusuk alas 6 cm. Jarak titik A ke TC adalah ….

A.   2√2 cm
B.   2√3 cm
C.   3√2 cm
D.   3√3 cm
E.   3√6 cm

Pembahasan

Perhatikan gambar limas beraturan T.ABCD berikut ini!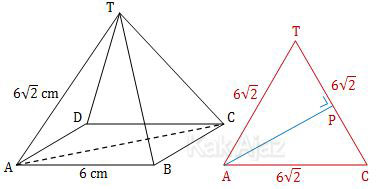

Pada gambar di atas, panjang AT = CT = 6√2 cm. Sedangkan AC merupakan diagonal alas persegi yang bersisi 6 cm sehingga panjang AC = 6√2 cm. Dengan demikian, segitiga ACT adalah segitiga sama sisi.

AP adalah jarak antara titik A ke garis CT. AP sama dengan tinggi segitiga sama sisi ACT.

AP = tinggi ΔACT
      = 1/2 a√3          [a: rusuk segitiga]
      = 1/2 ∙ 6√2 ∙ √3
      = 3√6

Jadi, Jarak titik A ke TC pada limas T.ABCD adalah 3√6 cm (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga]

Soal No. 32 tentang Sudut antara Garis dan Bidang pada Dimensi Tiga

Diketahui limas alas segiempat beraturan T.ABCD. panjang rusuk tegak = panjang rusuk alas = 4 cm. Sudut antara garis TA dan bidang alas ABCD adalah ….

A.   15°
B.   30°
C.   45°
D.   60°
E.   90°

Pembahasan

Perhatikan gambar limas T.ABCD di bawah ini!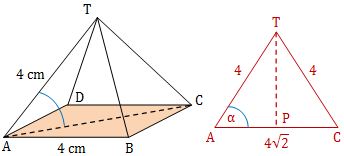

Berdasarkan gambar di atas, sudut α dapat dicari dari perbandingan antara AP dengan AT (kosinus), di mana AP adalah setengah AC.

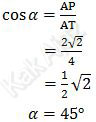
Jadi, Sudut antara garis TA dan bidang alas ABCD pada limas T.ABCD adalah 45° (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga]

Soal No. 33 tentang Transformasi Geometri

Persamaan peta garis 2x + 3y + 1 = 0 karena dilatasi [0, 3] dilanjutkan pencerminan terhadap garis y = x adalah ….

A.   3x + 2y + 3 = 0
B.   3x − 2y − 3 = 0
C.   2x + 3y − 3 = 0
D.   2x − 3y + 3 = 0
E.   2x + 2y + 3 = 0

Pembahasan

Misalkan:

T adalah matriks komposisi T₁ dilanjutkan T₂.

Persamaan matriks transformasi yang berlaku adalah:

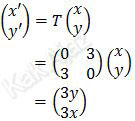
Diperoleh:

x' = 3y → y = 1/3 x'
y' = 3x → x = 1/3 y'

Sekarang kita substitusikan ke persamaan garis di atas.

                   2x + 3y + 1 = 0
2(1/3 y') + 3(1/3 x') + 1 = 0
                2/3 y' + x' + 1 = 0
                  2y' + 3x' + 3 = 0
                  3x' + 2y' + 3 = 0

Jadi, persamaan peta garis tersebut adalah opsi 3x + 2y + 3 = 0 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri.

Soal No. 34 tentang Persamaan Lingkaran

Persamaan lingkaran dengan pusat di titik (2, −3) dan menyinggung garis x = 5 adalah ….

A.   x² + y² + 4x − 6y + 9 = 0
B.   x² + y² − 4x + 6y + 9 = 0
C.   x² + y² − 4x + 6y + 4 = 0
D.   x² + y² − 4x − 6y + 9 = 0
E.   x² + y² + 4x − 6y + 4 = 0

Pembahasan

Gambar lingkaran yang dimaksud adalah sebagai berikut:

Karena garis x = 5 adalah garis lurus (tidak miring) maka jari-jari lingkaran tersebut merupakan selisih absis antara titik pusat dan garis.

r = 5 − 2
   = 3

Persamaan lingkaran dengan titik pusat (h, k) dan jari-jari r dirumuskan:

           (x − h)² + (y − k)² = r²
           (x − 2)² + (y + 3)² = 3²
x² − 4x + 4 + y² + 6y + 9 = 9
      x² + y² − 4x + 6y + 4 = 0

Jadi, persamaan lingkaran tersebut adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.

Soal No. 35 tentang Garis singgung Lingkaran

Salah satu persamaan garis singgung lingkaran x² + y² + 2x − 6y + 5 = 0 yang sejajar garis 2x − y + 7 = 0 adalah ….

A.   2x − y + 10 = 0
B.   2x − y + 5 = 0
C.   2x − y + 3 = 0
D.   2x + y + 1 = 0
E.   2x + y − 5 = 0

Pembahasan

Untuk menentukan garis singgung lingkaran, kita perlu data pusat lingkaran, jari-jari, dan gradien. Pusat dan jari-jari lingkaran dapat diperoleh dari persamaan lingkaran dengan membandingkan bentuk umumnya sebagai:

x² + y² + 2x − 6y + 5 = 0
x² + y² + 2Ax + 2By + C = 0   [bentuk umum]

Dengan membanding persamaan lingkaran dan bentuk umumnya, diperoleh:

2A = 2
  A = 1

2B = −6
  B = −3

C = 5

Pusat dan jari-jari lingkaran tersebut adalah:

Pusat : (−A, −B)
            (−1, 3) → (h, k)

Jari-jari : r = √(A² + B² − C)
                  = √(1² + (−3)² − 5)
                  = √5

Sedangkan gradien dapat diperoleh dari garis. Gradien garis ax + by + c = 0 dirumuskan:

m = −a/b

Sehingga gradien garis 2x − y + 7 = 0 adalah:

m = −2/(−1)
    = 2

Karena garis singgung lingkaran sejajar dengan garis, maka gradien garis singgung lingkaran sama dengan gradien garis tersebut.

Nah, sekarang kita tentukan persamaan garis singgung lingkaran tersebut.

y − k = m(x − h) ± r √(m² + 1)
y − 3 = 2(x + 1) ± √5 ∙ √(2² + 1)
         = 2x + 2 ± 5
      y = 2x + 5 ± 5

Persamaan garis singgung tersebut dapat dijabarkan menjadi:

y = 2x + 5 + 5
y = 2x + 10
2x − y + 10 = 0

atau

y = 2x + 5 − 5
y = 2x
2x − y = 0

Jadi, sesuai opsi jawaban yang tersedia, persamaan garis singgung lingkaran tersebut adalah (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.

Simak Pembahasan Soal Matematika IPA UN 2017 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.