Pembahasan Matematika IPA UN 2017 No. 6 - 10

Berbagai Fungsi dalam Matematika

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 6 sampai dengan nomor 10 tentang:

• invers fungsi, 
• komposisi fungsi, 
• sifat akar persamaan kuadrat, 
• jenis akar persamaan kuadrat, dan 
• persamaan kuadrat baru.

Soal No. 6 tentang Invers Fungsi

Jika fungsi

maka (g ∘ f)⁻¹(x) = ….

Pembahasan

Kita tentukan dulu komposisi (g ∘ f)(x). Pada komposisi tersebut fungsi g ada di depan, berarti kita harus berpatokan pada g(x).

Selanjutnya kita cari invers dari (g ∘ f)(x) dengan memanfaatkan rumus:

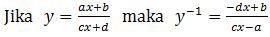
Dengan demikian,

Jadi, invers dari fungsi komposisi tersebut adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi.

Soal No. 7 tentang Komposisi Fungsi

Diketahui fungsi f ∶ R → R dan g ∶ R → R. Jika g(x) = 2x − 4 dan (g ∘ f) = 4x² − 24x + 32, fungsi f(−2) adalah ….

A.   12
B.   24
C.   32
D.   50
E.   95

Pembahasan

Berpedoman pada g(x) = 2x − 4 maka bisa diartikan (g ∘ f) = 2f(x) − 4.

    (g ∘ f) = 4x² − 24x + 32
2f(x) − 4 = 4x² − 24x + 32
      2f(x) = 4x² − 24x + 36
        f(x) = 2x² − 12x + 18

Nah, kita tinggal memasukkan x = −2 pada fungsi f(x) tersebut.

f(−2) = 2(−2)² − 12(−2) + 18
         = 8 + 24 + 18
         = 50

Jadi, nila dari f(−2) adalah 50 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi.

Soal No. 8 tentang Sifat Akar Persamaan Kuadrat

Akar-akar persamaan x² − 2x − (p + 5) = 0 adalah x₁ dan x₂, dengan x₁² + x₂² = 28. Nilai p yang memenuhi adalah ….

A.   −16
B.   −14
C.   −7
D.   7
E.   14

Pembahasan

Dari persamaan kuadrat x² − 2x − (p + 5) = 0 diperoleh:

a = 1
b = −2
c = −(p + 5)
   = −p − 5

Sifat-sifat akar persamaan kuadrat adalah sebagai berikut:

x₁ + x₂ = −b/a
            = 2

x₁ ⋅ x₂ = c/a
           = −p − 5

Sementara itu diketahui pada soal:

x₁² + x₂² = 28

Jumlah kuadrat akar tersebut bisa dijabarkan menjadi:

(x₁ + x₂)² − 2 x₁⋅x₂ = 28

Nah, sekarang kita tinggal memasukkan sifat penjumlahan dan perkalian akar di atas.

2² − 2(–p − 5) = 28
    4 + 2p + 10 = 28
                   2p = 14
                     p = 7

Jadi, nilai p yang memenuhi persamaan kuadrat tersebut adalah 7 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan dan Fungsi Kuadrat.

Soal No. 9 tentang Jenis Akar Persamaan Kuadrat

Jika persamaan kuadrat x² + (p +1 )x +( 2 − p) = 0 memiliki akar-akar yang tidak real, nilai p yang memenuhi persamaan tersebut adalah ….

A.   −1 < p < 7
B.   −7 < p < 1
C.   −7 ≤ p ≤ 1
D.   p ≤ −7 atau p ≥ 7
E.   p < −7 atau p > 7

Pembahasan

Dari persamaan kuadrat x² + (p +1 )x +( 2 − p) = 0 diperoleh:

a = 1
b = p + 1
c = 2 − p

Persamaan kuadrat yang akar-akarnya tidak real mempunyai diskriminan negatif.

                               D < 0
                    b² − 4ac < 0
(p + 1)² − 4∙1∙(2 − p) < 0
 p² + 2p + 1 − 8 + 4p < 0
                p² + 6p − 7 < 0
            (p + 7)(p − 1) < 0

Karena tanda pertidaksamaannya ‘<’ maka penyelesaiannya berada di antara −7 dan 1.

−7 < p < 1

Jadi, nilai p yang memenuhi persamaan kuadrat tersebut adalah opsi (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan dan Fungsi Kuadrat.

Soal No. 10 tentang Persamaan Kuadrat Baru

Akar-akar persamaan kuadrat 3x² − x − 5 = 0 adalah x₁ dan x₂. Persamaan kuadrat baru yang akar-akarnya (3x₁ − 1) dan (3x₁ − 1) adalah ….

A.   x² + x − 17 = 0
B.   x² + x + 13 = 0
C.   x² + x − 15 = 0
D.   x² − x − 15 = 0
E.   x² − x + 15 = 0

Pembahasan

Penjumlahan dan perkalian akar persamaan kuadrat 3x² − x − 5 = 0 yang akar-akarnya x₁ dan x₂ adalah:

x₁ + x₂ = −b/a
            = 1/3

x₁ ⋅ x₂ = c/a
           = −5/3

Misalkan persamaan kuadrat baru yang akar-akarnya (3x₁ − 1) dan (3x₁ − 1) adalah:

x² − px + q = 0

dengan p adalah hasil jumlah akar-akar baru sedangkan q adalah hasil kali akar-akar baru.

p = (3x₁ − 1) + (3x₁ − 1)
   = 3(x₁ + x₂) − 2
   = 3 ∙ 1/3 − 2
   = −1

q = (3x₁ − 1) (3x₁ − 1)
   = 9x₁⋅x₂ − 3x₁ − 3x₂ + 1
   = 9x₁⋅x₂ − 3(x₁ + x₂) + 1
   = 9 ∙ (−5/3) − 3 ∙1 /3 + 1
   = −15 − 1 + 1
   = −15

Dengan demikian, persamaan kuadrat baru yang dimaksud adalah:

x² − px + q = 0
x² + x − 15 = 0

Jadi, persamaan kuadrat baru yang akar-akarnya (3x₁ − 1) dan (3x₁ − 1) adalah x² + x − 15 = 0 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan dan Fungsi Kuadrat.

Simak Pembahasan Soal Matematika IPA UN 2017 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.