Pembahasan Matematika SMP UN 2019 No. 16 - 20 Paket 2

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2019 Paket 2 nomor 16 sampai dengan nomor 20 tentang:

• sistem persamaan linear, 
• persamaan linear satu variabel, 
• diagram Venn, 
• fungsi, dan 
• penerapan sistem persamaan linear.

Soal No. 16 tentang Sistem Persamaan Linear

Diketahui persamaan 4x + 7y = 2 dan 3x + 2y = −5. Nilai dari 2x − 3y adalah ….

A.	−12
B.	−1
C.	0
D.	3

Pembahasan

Eliminasi dari dua persamaan tersebut adalah:

4x + 7y	=	2	|×3|
3x + 2y	=	−5	|×4|

12x + 21y	=	6
12x + 8y	=	−20
			−
13y	=	26
y	=	2

Substitusi y = 2 ke persamaan yang pertama, diperoleh:

4x + 7 × 2	=	2
4x + 14	=	2
4x	=	−12
x	=	−3

Dengan demikian,

2x − 3y	=	2 × (−3) − 3 × 2
	=	−6 − 6
	=	−12

Jadi, nilai dari 2x − 3y adalah −12 (A).

Soal No. 17 tentang Persamaan Linear Satu Variabel

Diketahui m adalah penyelesaian dari persamaan 3x + 1/2 = 4⅓ x − 1/6. Nilai dari m + 5 adalah ….

A.	½
B.	2
C.	5½
D.	7

Pembahasan

Kita lakukan penyederhanaan pecahan dulu.

3x + 1/2 = 4⅓ x − 1/6
3x + 1/2 = 13/3 x − 1/6

Karena persamaan linear tersebut mempunyai penyebut 6, 3, dan 2, maka semua sukunya kita kalikan dengan 6, sehingga:

18x + 3	=	26x − 1
−8x	=	−4
x	=	−4/(−8)
	=	1/2

Nilai x ini disebut m, sehingga

m + 5	=	1/2 + 5
	=	5½

Jadi, nilai dari m + 5 adalah 5½ (C).

Soal No. 18 tentang Diagram Venn

Seleksi pengurus OSIS di SMP “Bhinneka Tunggal Ika” menggunakan aturan yaitu siswa yang dapat diterima sebagai pengurus adalah mereka yang lulus tes tertulis dan wawancara. Dari 62 pendaftar, peserta yang dinyatakan lulus tes tertulis sebanyak 52 siswa yang dinyatakan lulus tes wawancara sebanyak 43 siswa, dan 2 siswa tidak mengikuti seleksi karena berhalangan.

Banyak siswa yang diterima sebagai pengurus OSIS adalah ….

A.	25 anak
B.	31 anak
C.	33 anak
D.	35 anak

Pembahasan

Siswa yang diterima sebagai pengurus OSIS adalah siswa yang lulus tes tertulis dan tes wawancara.

Jika x adalah banyak siswa yang diterima sebagai pengurus OSIS maka diagram Venn untuk soal di atas adalah:

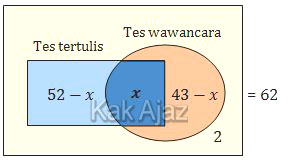
Berdasarkan diagram Venn di atas, berlaku persamaan:

(52 − x) + x + (43 − x) + 2	=	62
97 − x	=	62
97 − 62	=	x
x	=	35

Jadi, banyak siswa yang diterima sebagai pengurus OSIS adalah 35 anak (D).

Soal No. 19 tentang Fungsi

Diketahui fungsi f(x) = ax + b. Jika f(−2) = −11 dan f(4) = 7, nilai a + b adalah ….

A.	3
B.	−2
C.	−5
D.	−8

Pembahasan

Dengan berpedoman pada fungsi f(x), maka fungsi f(−2) dapat kita cari dengan menggantikan x pada f(x) dengan −2. Demikian juga untuk menentukan f(4) dapat dilakukan dengan menggantikan x dengan 4.

Perhatikan penentuan f(−2) dan f(4) berikut ini!

f(x)	=	ax + b
f(−2)	=	−2a + b = −11 ... (1)
f(4)	=	4a + b = 7       ... (2)

Kemudian kita eliminasikan persamaan (1) dan (2).

−2a + b	=	−11
4a + b	=	7
			−
−6a	=	−18
a	=	3

Selanjutnya, kita substitusikan a = 3 ke persamaan (1) untuk mendapatkan nilai b.

−2a + b	=	−11
−2×3 + b	=	−11
−6 + b	=	−11
b	=	−5

Dengan demikian.

a + b	=	3 + (−5)
	=	−2

Jadi, nilai a + b adalah −2 (B).

Soal No. 20 tentang Penerapan Sistem Persamaan Linear

Harga sepasang sepatu dua kali harga sepasang sandal. Ardi membeli 2 pasang sepatu dan 3 pasang sandal dengan harga Rp420.000,00. Jika Doni membeli 3 pasang sepatu dan 2 pasang sandal, Doni harus membayar sebesar ….

A.	Rp180.000,00
B.	Rp360.000,00
C.	Rp480.000,00
D.	Rp540.000,00

Pembahasan

Jika x adalah harga sepasang sepatu dan y adalah harga sepasang sandal maka diperoleh model matematika sebagai berikut:

x	=	2y	… (1)
2x + 3y	=	420.000	… (2)

Substitusi persamaan (1) ke persamaan (2), diperoleh:

2x + 3y	=	420.000
2 ∙ 2y + 3y	=	420.000
7y	=	420.000
y	=	60.000

Selanjutnya kita substitusikan y = 60.000 ke persamaan (1), diperoleh:

x	=	2y
	=	2 × 60.000
	=	120.000

Harga yang harus dibayar jika Doni membeli 3 pasang sepatu dan 2 pasang sandal adalah:

3x + 2y	=	3 × 120.000 + 2 × 60.000
	=	360.000 + 120.000
	=	480.000

Jadi, Doni harus membayar sebesar Rp480.000,00 (C).

Simak Pembahasan Soal Matematika SMP UN 2019 Paket 2 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.