Pembahasan Matematika IPA UN 2014 No. 21

Pembahasan soal Matematika UN 2014 program studi IPA nomor 21 sampai dengan nomor 25 tentang:

deret geometri,
jarak titik ke garis,
sudut antara garis dan bidang,
aturan sinus dan kosinus, serta
persamaan trigonometri.

Soal No. 21 tentang Deret Geometri

Seutas tali dipotong menjadi 5 bagian sehingga panjang potongan-potongan tali tersebut membentuk barisan geometri. Jika panjang tali terpendek 6 cm dan potongan tali terpanjang 96 cm maka panjang tali semula adalah ....

A.   96 cm
B.   185 cm
C.   186 cm
D.   191 cm
E.   192 cm

Pembahasan

Data yang diketahui pada soal:

deret geometri
n = 5
U₁ = 6 cm
U₅ = 96 cm

Sedangkan yang ditanyakan pada soal adalah S₅. Kita tentukan rasio deret geometri tersebut.

$Rumus rasio (pengali) deret geometri atau deret ukur$
$Penghitungan rasio deret geometri$

Karena nilai r > 1 maka rumus jumlah deret geometri yang kita gunakan adalah:

$Rumus jumlah deret geometri dengan r > 1, jumlah n suku pertama$
$Penghitungan jumlah deret geometri$

Jadi, panjang tali semula adalah 186 cm (C).

Persdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 22 tentang Dimensi Tiga (jarak titik ke garis)

Diketahui kubus ABCD.EFGH dengan rusuk 9 cm. Jika T terletak pada pertengahan garis HF, jarak titik A ke garis CT adalah ....

A. 5√3 cm
B. 6√2 cm
C. 6√3 cm
D. 6√6 cm
E. 7√3 cm

Pembahasan

Kita gambar dulu kubusnya supaya memahami persoalannya.

Jarak titik A ke garis CT dalam kubus ABCD.EFGH

Sekarang, pandanglah diagonal bidang ACGE!

menentukan jarak titik dan garis dengan memandang diagonal ACGE

Garis CT dan garis ET' adalah dua garis yang sejajar dan sama-sama menghubungkan titik tengah dan titik sudut ACGE. Dua garis ini ternyata membagi garis AG menjadi tiga bagian yang sama panjang sehingga AA' = 2/3 AG. Sedangkan AG merupakan diagonal ruang kubus ABCD.EFGH yang terkenal dengan rumus a√3 dengan a adalah sisi kubus.

AG = a√3
      = 9√3

AA' = 2/3 AG
       = 2/3 × 9√3
       = 6√3

Jadi, jarak titik A ke garis CT adalah 6√3cm (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga].

Soal No. 23 tentang Dimensi Tiga (sudut antara garis dan bidang)

Kubus ABCD.EFGH mempunyai rusuk 4 cm. Sudut antara AE dan bidang AFH adalah α. Nilai sin α = ....

A.   ½√2
B.   ½√3
C.   ⅓√3
D.   ⅔√2
E.   ¾√3

Pembahasan

Perhatikan gambar berikut ini!

Sudut antara garis AE dan bidang AFH pada kubus ABCD.EFGH

Untuk menentukan sudut yang dibentuk oleh garis AE dan bidang AFH, kita tentukan dulu titik pertemuan antara garis dan bidang tersebut, yaitu titik A.

Dari titik A, kita tarik garis tengah bidang AFH, yaitu garis AT. Sudut yang dibentuk oleh garis AE dan garis AT inilah yang disebut sudut α.

ET adalah setengah diagonal EG. Sedangkan EG adalah diagonal bidang kubus yang dikenal dengan rumus a√2.

EG = a√2
      = 4√2

ET = ½ EG
      = ½ 4√2 cm
      = 2√2 cm

Sekarang, pandanglah segitiga AET!

pada segitiga siku-siku AET hukum Pythagoras dan trigonometri

Segitiga AET adalah segitiga siku-siku sehingga berlaku teorema Pythagoras dan trigonometri.

$Teorema Pythagoras pada segitiga siku-siku$

Coba masing-masing suku dalam akar dibagi 2². Diperoleh:

$AT=2\sqrt{2^{2}+(\sqrt{2})^{2}}=2\sqrt{6}$

Sekarang kita tentukan nilai sinus sudutnya.

$Rumus sinus sudut dalam segitiga siku-siku$

Jadi, nilai sin α = ⅓√3 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga].

Soal No. 24 tentang Trigonometri (aturan sinus dan kosinus)

Diketahui segiempat ABCD seperti gambar.

trigonometri: aturan sinus dan kosinus segitiga

Panjang sisi BC adalah ....

A. 7√3 cm
B. 6√3 cm
C. 4√5 cm
D. 3√5 cm
E. 2√5 cm

Pembahasan

Pandanglah segitiga ABD!

Data pada segitiga tersebut adalah dua sudut dan satu sisi. Karena itu, gunakan aturan sinus untuk menentukan sisi BD.

$Aturan sinus segitiga$
$\frac{BD}{\frac{1}{2}\sqrt{3}}=\frac{2\sqrt{3}}{\frac{1}{2}}$

Angka ½ pada masing-masing bisa dicoret kemudian dikalikan silang. Diperoleh:

BD = 6 cm

Selanjutnya, pandanglah segitiga BCD!

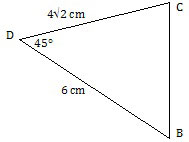
Karena pada segitiga tersebut diketahui satu sudut dan dua sisi, kita gunakan aturan kosinus untuk menentukan nilai BC.

BC² = BD² + CD² − 2 BD . CD cos 45
= 36 + 32 − 2 . 6 . 4√2 . ½√2
= 20
BC = 2√5

Jadi, panjang sisi BC adalah 2√5 cm (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus.

Soal No. 25 tentang Trigonometri (persamaan trigonometri)

Himpunan penyelesaian dari persamaan 2 sin x − √3 = 0 untuk 0 ≤ x ≤ 2π adalah ....

A. {⅓π, ⅔π}
B. {⅓π, ⅙π}
C. {⅓π, ½π}
D. {⅓π, ⅚π}
E. {⅔π, ⅚π}

Pembahasan

Untuk menyelesaikan soal persamaan trigonometri, selain harus hafal sudut-sudut istimewa juga harus memperhatikan daerah atau interval sudut yang ditanyakan.

2 sin x − √3 = 0
sin x = ½ √3
sin x = sin 60°

Pada interval 0 ≤ x ≤ 2π, nilai sin x = ½ √3 (positif) terdapat pada kuadran I dan II.

Kuadran I
$arc sin x pada kuadran I$

Kuadran II
$arc sin x pada kuadran II$

Jadi, himpunan penyelesaian dari persamaan trigonometri tersebut adalah opsi (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Trigonometri.

Simak Pembahasan Soal Matematika IPA UN 2014 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

Thursday, 5 November 2015