- komposisi dan invers fungsi,
- persamaan linear,
- matriks,
- operasi vektor, serta
- sudut antara dua vektor.
Soal No. 11 tentang Komposisi dan Invers Fungsi
Diketahui fungsi f(x) = 2x + 1 dan g(x) = (x + 1)/x, x ≠ 0. Invers fungsi (f o g)(x) adalah (f o g)−1(x) = ....
%5E%7B-1%7D(x)=%5Cfrac%7B2x%7D%7Bx-3%7D,%5C,&space;%5C,&space;%5C,&space;x%5Cneq&space;3)
%5E%7B-1%7D(x)=%5Cfrac%7B2x%7D%7Bx+3%7D,%5C,&space;%5C,&space;%5C,&space;x%5Cneq&space;-3)
%5E%7B-1%7D(x)=%5Cfrac%7B2%7D%7Bx-3%7D,%5C,&space;%5C,&space;%5C,&space;x%5Cneq&space;3)
%5E%7B-1%7D(x)=%5Cfrac%7B2%7D%7Bx+3%7D,%5C,&space;%5C,&space;%5C,&space;x%5Cneq&space;-3)
%5E%7B-1%7D(x)=%5Cfrac%7Bx-2%7D%7Bx+3%7D,%5C,&space;%5C,&space;%5C,&space;x%5Cneq&space;-3)
Pembahasan
Komposisi fungsi (f o g)(x) biasanya dibaca "f bundaran g". Artinya, di dalam fungsi f terkandung fungsi g(x) atau fungsi g(x) tersarang dalam fungsi f.f(x) = 2x + 1
(f o g)(x) = f[g(x)]
= 2g(x) + 1
f[g(x)] = 2g(x) + 1 mengikuti pola f(x) = 2x + 1. Sekarang kita operasikan fungsi g(x) pada komposisi fungsi tersebut.
(f o g)(x) = 2g(x) + 1
Untuk menentukan fungsi inversnya kita gunakan rumus berikut ini.
Berdasarkan rumus tersebut, diperoleh:
Jadi, invers komposisi fungsi tersebut adalah opsi (C).
Perdalam materi ini di Pembahasan Soal UN: Komposisi dan Invers Fungsi.
Soal No. 12 tentang Persamaan Linear
Di Zedland ada dua media massa koran yang sedang mencari orang untuk bekerja sebagai penjual koran. Iklan di bawah ini menunjukkan bagaimana mereka membayar gaji penjual koran.

Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Media Zedland atau Harian Zedland. Grafik manakah di bawah ini yang menggambarkan bagaimana koran membayar penjual-penjualnya?


Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Media Zedland atau Harian Zedland. Grafik manakah di bawah ini yang menggambarkan bagaimana koran membayar penjual-penjualnya?


Pembahasan
Kita ambil permisalan terlebih dahulu.x : jumlah koran yang terjual per minggu
y : pendapatan per minggu
Pendapatan penjual koran di Media Zedland:
- 240 koran pertama yang terjual mendapat gaji 0,2 zed per koran = 0,2x.
- Setelah 240, setiap koran yang terjual mendapat gaji 0,4 zed per koran = 0,4x.
Grafiknya terdiri dari dua garis yang berbeda kemiringan (gradien 0,2 dan 0,4) yang berawal dari pangkal koordinat (ditunjukkan oleh garis biru).

Pendapatan penjual koran di Harian Zedland.
- Gaji tetap 60 zed.
- Bonus 0,05 zed tiap koran terjual = 0,05x.
y = 60 + 0,05x
Grafiknya berupa garis lurus naik yang berawal dari y = 60 (garis merah).
Jadi, yang menggambarkan pendapatan penjual koran di masing-masing koran adalah grafik (C).
Soal No. 13 tentang Matriks
Diketahui matriks:
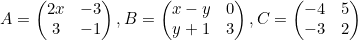
Jika Ct adalah transpose dari matriks C dan A + B = Ct, nilai dari 3x + 2y = ....
A. −1
B. −7
C. −11
D. −14
E. −25
Jika Ct adalah transpose dari matriks C dan A + B = Ct, nilai dari 3x + 2y = ....
A. −1
B. −7
C. −11
D. −14
E. −25
Pembahasan
Transpose matriks adalah matriks yang mengalami pertukaran baris menjadi kolom dan kolom menjadi baris dari matriks sebelumnya.A + B = Ct
Penjumlahan matriks adalah penjumlahan elemen-elemen matriks yang bersesuaian, kanan-atas dijumlah dengan kanan-atas, dan seterusnya. Diperoleh:
Ini adalah bentuk kesamaan matriks. Setiap elemen yang bersesuaian pada kedua matriks tersebut mempunyai nilai yang sama. Akan kita tentukan nilai x dan y. Temukan terlebih dahulu elemen yang hanya terdiri dari satu variabel. Ya, komponen yang terletak pada kiri-bawah.
y + 4 = 5
y = 1
Selanjutnya kita tentukan nilai x dari komponen yang letaknya kiri-atas.
3x − y = −4
3x − 1 = −4
3x = −3
x = −1
Dengan demikian nilai dari:
3x + 2y = 3.(−1) + 2.1
= −3 + 2
= −1
Jadi, nilai dari 3x + 2y adalah −1 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks.
Soal No. 14 tentang Operasi Vektor
Diketahui vektor:
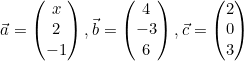
Jika a tegak lurus b, hasil dari (3a − b) + 2c adalah ....
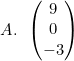
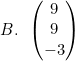
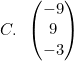
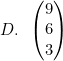
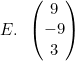
Jika a tegak lurus b, hasil dari (3a − b) + 2c adalah ....
Pembahasan
Jika a tegak lurus b maka perkalian dot antara a dan b sama dengan nol.a . b = 0
4x − 6 − 6 = 0
4x = 12 → x = 3
Sehingga komponen-komponen vektor a menjadi:
Dengan demikian, nilai dari (3a − b) + 2c dapat ditentukan.
3a − b + 2c =
Jadi, hasil operasi vektor tersebut adalah opsi (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Operasi Vektor.
Soal No. 15 tentang Sudut antara Dua Vektor
Diketahui vektor-vektor u = −12i + aj +bk dan v = ai − bj + ak. Sudut antara u dan v adalah θ dengan cos θ = ¼√3. Proyeksi u pada v adalah p = −4i + 4j − 4k. Nilai dari b = ....
A. 4√7
B. 2√14
C. 2√7
D. √14
E. √7
A. 4√7
B. 2√14
C. 2√7
D. √14
E. √7
Pembahasan
p adalah proyeksi u pada v, berarti p searah dengan v. Hal ini juga berarti bahwa p merupakan kelipatan dari v.p = k v
Berdasarkan kesamaan matriks baris ke-1 dan ke-2 diperoleh:
baris ke-1 : −4 = ka
4 = −ka
baris ke-2 : 4 = −kb
Sehingga ka = kb atau a = b.
Selanjutnya kita gunakan rumus sudut (cos θ) antara vektor u dan v. Sebelumnya kita tentukan dulu besaran-besaran yang diperlukan pada rumus tersebut. Karena a = b dan yang ditanyakan b maka rumus-rumus berikut ini dinyatakan dalam b.
u = (−12, a, b)
= (−12, b, b)
v = (a, −b, a)
= (b, −b, b)
u.v = −12b − b2 + b2
= −12b
Nah, sekarang kita terapkan pada rumus sudut vektor.
Secara matematis, soal ini kurang valid. Hasil akar tidak mungkin negatif.
Ok, pura-pura tidak tahu. Kita kuadratkan masing-masing ruas.
144 + 2b2 = 256
2b2 = 112
b2 = 56
b = 2√14
Jadi, nilai b pada vektor tersebut adalah 2√14 (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Dua Vektor.
Simak Pembahasan Soal Matematika IPA UN 2014 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan