Pembahasan Matematika SMP UN 2015 No. 16 - 20

Pembahasan soal Matematika SMP Ujian Nasional tahun 2015 nomor 16 sampai dengan nomor 20 tentang:

• fungsi, 
• gradien garis, 
• persamaan garis, 
• sistem persamaan linear dua variabel, serta 
• penerapan sistem persamaan linear dua variabel.

Soal No. 16 tentang Fungsi

Diketahui rumus fungsi f(x) = 3x − 7. Nilai f(a + 3) adalah ….

A.   3a + 16
B.   3a + 2
C.   3a − 2
D.   3a − 16

Pembahasan

Diketahui f(x) ditanyakan f(a + 3) berarti mengganti variabel x dengan a + 3. 

      f(x) = 3x − 7 
f(a + 3) = 3(a + 3) − 7
             = 3a + 9 − 7
             = 3a + 2

Jadi, nilai dari f(a + 3) adalah 3a + 2 (B).

Soal No. 17 tentang Gradien Garis

Gradien garis 3y − 6x = −8 adalah ….

A.   2
B.   1/2
C.   −1/2
D.   −2

Pembahasan

Gradien garis 3y − 6x = −8 secara sederhana dapat dirumuskan sebagai:



dengan a adalah koefisien x sedangkan b adalah koefisien y dengan syarat x dan y berada dalam satu ruas. 

a = −6 
b = 3

Dengan demikian, nilai gradien garis tersebut adalah:


      = 2

Jadi, gradien garis tersebut adalah 2 (A).

Soal No. 18 tentang Persamaan Garis

Suatu perusahaan taksi memasang tarif seperti grafik berikut.

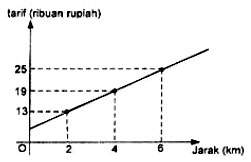
Alia pergi ke rumah nenek yang berjarak 22 kilometer dengan menggunakan taksi tersebut. Berapa tarif taksi yang harus dibayar Alia?

A.   Rp66.000,00.
B.   Rp73.000,00.
C.   Rp132.000,00.
D.   Rp143.000,00.

Pembahasan

Langkah pertama adalah menentukan persamaan tarif taksi berdasarkan grafik di atas. Misal y = tarif dan x = jarak, berlaku: 

y = mx + c

dengan m adalah gradien dan c adalah ordinat titik potong pada sumbu y.

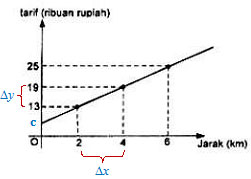
Berdasarkan grafik tersebut diperoleh:


    
     = 6/2
     = 3

19 − 13 = 13 − c
           6 = 13 − c
            c = 13 − 6
              = 7

Dengan demikian, persamaan tarif taksi tersebut adalah:

y = mx + c
y = 3x + 7

Jika Alia menempuh jarak 22 km (x = 22) maka tarif taksinya adalah: 

y = 3×22 + 7
   = 66 + 7
   = 73   (dalam ribuan rupiah)

Jadi, tarif taksi yang harus dibayar Alia adalah Rp73.000,00 (B).

Soal No. 19 tentang Penerapan Sistem Persamaan Linear Dua Variabel

Adi, Budi, dan Citra bersama-sama membeli buku tulis dan pensil yang sejenis. Adi membeli 4 buku tulis dan 1 pensil seharga Rp14.000,00. Budi membeli 6 buku tulis dan 2 pensil seharga Rp22.000,00. Jika Citra membeli 5 buku tulis dan 1 pensil, berapa rupiah yang harus dibayar Citra?

A.   Rp13.000,00.
B.   Rp16.750,00.
C.   Rp17.000,00.
D.   Rp18.000,00.

Pembahasan

Kita buat permisalan terlebih dahulu. 

x : buku tulis 
y : pensil

Model matematika alat tulis yang dibeli oleh Adi, Budi, dan Citra adalah

Adi   : 4x + y   = 14.000
Budi : 6x + 2y = 22.000
Citra : 5x + y   = ?

Nah, sekarang mari kita selesaikan model matematika di atas dengan cara eliminasi dan substitusi.

4x + y   = 14.000  |×1 |  4x + y = 14.000
6x + 2y = 22.000  |×½|  3x + y = 11.000
                                          ———————  −
                                              x = 3.000 

x = 3.000 →            4x + y = 14.000
                       4×3.000 + y = 14.000
                         12.000 + y = 14.000 
                                        y = 2.000

Dengan demikian, harga alat tulis yang dibeli Citra adalah:

5x + y = 5×3.000 + 2.000
           = 15.000 + 2.000
           = 17.000

Jadi, harga 5 buku tulis dan 1 pensil yang dibeli oleh Citra adalah Rp17.000,00 (C).

Soal No. 20 tentang Sistem Persamaan Linear Dua Variabel

Penyelesaian dari ¾ x − ⅓ y = 2 dan ½ x + ⅔ y = 4 adalah x = a dan y = b. Nilai a − 3b adalah ….

A.   −8
B.   −5
C.   1
D.   5

Pembahasan

Soal di atas kelihatan sulit karena koefisiennya berbentuk pecahan. Untuk mengatasinya kita kalikan masing-masing suku dengan suatu bilangan. Bilangan tersebut haruslah merupakan hasil kali penyebutnya.

¾ x − ⅓ y = 2  |×12|  9x − 4y = 24
½ x + ⅔ y = 4  | × 6|  3x + 4y = 24
                                     —————— +
                                        12x = 48
                                            x = 4 

x = 4 →      3x + 4y = 24
                 3×4 + 4y = 24
                   12 + 4y = 24
                           4y = 12
                             y = 3

Sekarang kita masuk ke pertanyaan. 

a − 3b = x − 3y
            = 4 − 3×3
            = 4 − 9
            = −5

Jadi, nilai dari a − 3b adalah −5 (B).

Simak Pembahasan Soal Matematika SMP UN 2015 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.