Pembahasan Matematika IPA UN 2016 No. 11 - 15

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPA nomor 11 sampai dengan nomor 15 tentang:

• pembagian suku banyak, 
• akar-akar suku banyak, 
• operasi matriks, 
• determinan matriks, dan 
• barisan aritmetika.

Soal No. 11 tentang Pembagian Suku Banyak

Suku banyak f(x) = 2x³ − 5x² + ax + 18 habis dibagi oleh (x − 3). Hasil bagi f(x) oleh (x + 1) adalah ....

A.   2x² − 7x + 2
B.   2x² + 7x − 2
C.   2x² − 7x − 2
D.   2x² − 6x − 3
E.   2x² − 6x + 3

Pembahasan

Suku banyak f(x) = 2x³ − 5x² + ax + 18 habis dibagi oleh (x − 3), berarti sisanya 0 atau f(3) = 0. Gunakan cara Horner untuk pembagian tersebut.

Perhatikan kolom terakhir. Kita dapat mendapatkan nilai a dari kolom tersebut.

18 + 3a + 9 = 0
              3a = −27
                a = −9

Sehingga suku banyak tersebut menjadi:

f(x) = 2x³ − 5x² − 9x + 18

Suku banyak f(x) ini kemudian dibagi (x + 1).

Hasil bagi pembagian suku banyak tersebut adalah:

      2    −7    −2
⇔  2x² − 7x − 2

Jadi, hasil bagi f(x) oleh (x + 1) adalah 2x² − 7x − 2 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Suku Banyak.

Soal No. 12 tentang Akar-akar Suku Banyak

Diketahui (x − 2) dan (x + 1) adalah faktor-faktor persamaan suku banyak x³ + ax² + bx + 10 = 0. Jika x₁, x₂, dan x₃ adalah akar-akar persamaan tersebut dengan x₁ < x₂ < x₃, nilai 2x₁ − x₂ + x₃ adalah ....

A.   −2
B.   1
C.   2
D.   5
E.   9

Pembahasan

(x − 2) dan (x + 1) adalah faktor-faktor dari suku banyak x³ + ax² + bx + 10 = 0. Ini berarti suku banyak tersebut habis dibagi oleh (x − 2) dan (x + 1). Kita gunakan cara Horner untuk pembagian tersebut.

Kita gunakan cara Horner bersusun seperti di atas karena semua sisa pembagian sama dengan nol. Jika sisa pembagian tidak sama dengan nol maka harus melakukan cara Horner satu per satu seperti pembahasan soal nomor 11.

Sekarang perhatikan kolom terakhir yang atas maupun yang bawah. Dari kedua kolom tersebut kita akan mendapatkan nilai a.

10 + a − b − 1 = 0
               a − b = − 9      ...(1)

−a + b + 1 + 2a + 2 = 0
                       a + b = −3 ...(2)

Selanjutnya kita eliminasikan persamaan (1) dan (2).

a − b = − 9
a + b = −3
⎯⎯⎯⎯⎯⎯⎯ +
     2a = −12
       a = −6

Nah, sekarang perhatikan baris terakhir skematik Horner di atas yang berwarna hijau. Itu adalah hasil bagi yang merupakan faktor lain dari suku banyak tersebut. Substitusikan a = −6 pada baris tersebut.

    1     a + 1
=  1    −6 + 1
=  1     −5
⇔ x − 5

Sehingga diperoleh:

faktor : (x + 1), (x − 2), (x − 5)
akar   : x₁ = −1, x₂ = 2, x₃ = 5

Dengan demikian,

2x₁ − x₂ + x₃ = 2×(−1) − 2 + 5
                      = −2 − 2 + 5
                      = 1

Jadi, nilai dari 2x₁ − x₂ + x₃ adalah 1 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Suku Banyak.

Soal No. 13 tentang Operasi Matriks

Diketahui persamaan matriks:

Nilai 2x − 3y = ....

A.   −19
B.   −17
C.   −13
D.   −7
E.   −4

Pembahasan

Modal mengerjakan soal di atas adalah mengingat kembali operasi penjumlahan dan perkalian matriks.

Dari kesamaan matriks di atas diperoleh:

Komponen kiri atas:
2x + 1 = 3
      2x = 2
        x = 1

Komponen kanan atas:
13 = 3 + 2y
2y = 10
  y = 5

Dengan demikian,

2x − 3y = 2×1 − 3×5
             = 2 − 15
             = −13

Jadi, nilai dari 2x − 3y adalah −13 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks.

Soal No. 14 tentang Determinan Matriks

Diketahui persamaan matriks

dengan matriks X berordo 2 × 2. Determinan matriks X adalah ....

A.   13
B.   28
C.   37
D.   53
E.   71

Pembahasan

Untuk menyelesaikan soal di atas, pahami konsep berikut ini!

Untuk A, B, dan C adalah matriks,

   AB = C
      A = C.B⁻¹
det A = (det C)/(det B)

Berdasarkan konsep di atas, diperoleh:

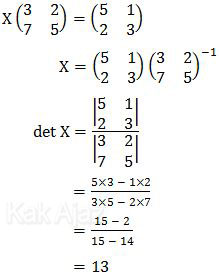
Jadi, determinan matriks X adalah 13 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Matriks.

Soal No. 15 tentang Barisan Aritmetika

Suatu barisan aritmetika memiliki suku kedua adalah 8, suku keempat adalah 14, dan suku terakhir 23. Jumlah semua suku barisan tersebut adalah ....

A.   56
B.   77
C.   98
D.   105
E.   112

Pembahasan

Diketahui:

U₂ = 8
U₄ = 14
U_n = 23

Dengan memanfaatkan rumus suku ke-n diperoleh:

U_n = a + (n − 1)b
U₂ = a + b = 8     ... (1)
U₄ = a + 3b = 14 ... (2)

Eliminasi persamaan (2) dan (1) diperoleh:

a + 3b = 14
a +   b = 8
⎯⎯⎯⎯⎯⎯⎯  −
       2b = 6
         b = 3

Substitusi b = 3 ke persamaan (1) diperoleh:

a + b = 8
a + 3 = 8
      a = 5

Sekarang kita tentukan banyaknya suku pada barisan aritmetika tersebut.

              U_n = 23
a + (n − 1)b = 23
5 + (n − 1)3 = 23
   5 + 3n − 3 = 23
                3n = 21
                  n = 7

Dengan demikian, jumlah ke-7 suku deret aritmetika tersebut adalah:

S_n = ½n(a + U_n)
S₇ = ½ × 7(5 + 23)
     = ½ × 7 × 28
     = 98

Jadi, jumlah semua suku barisan tersebut adalah 98 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.