Pembahasan Matematika IPA UN 2016 No. 21 - 25

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPA nomor 21 sampai dengan nomor 25 tentang:

• aturan sinus dan kosinus, 
• dimensi tiga (jarak titik ke garis), 
• dimensi tiga (sudut antara garis dan bidang), 
• transformasi geometri, serta 
• lingkaran.

Soal No. 21 tentang Aturan Sinus dan Kosinus

Sebuah kapal mulai bergerak dari pelabuhan A pada pukul 07.00 dengan arah 030° dan tiba di pelabuhan B setelah 4 jam bergerak. Pukul 12.00 kapal bergerak kembali dari pelabuhan B menuju pelabuhan C dengan memutar haluan 150° dan tiba di pelabuhan C pukul 20.00. Kecepatan rata-rata kapal 50 mil/jam.

Jarak tempuh kapal dari pelabuhan C ke pelabuhan A adalah ....

A.   200√2 mil
B.   200√3 mil
C.   200√6 mil
D.   200√7 mil
E.   600 mil

Pembahasan

Diketahui:

t_AB = 4 jam
t_BC = 20.00 − 12.00
      = 8 jam
  v  = 50 mil/jam

Jarak tempuh dari pelabuhan A ke pelabuhan B adalah:

s_AB = v . t_AB
       = 50 mil/jam × 4 jam
       = 200 mil

Sedangkan jarak tempuh dari pelabuhan B ke pelabuhan C adalah:

s_BC = v . t_BC
       = 50 mil/jam × 8 jam
       = 400 mil

Perhatikan perjalanan kapal berikut ini!

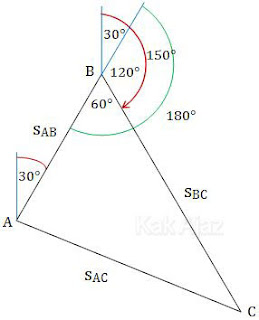
Berdasarkan gambar di atas, jarak tempuh kapal dari pelabuhan C ke pelabuhan A (s_AC) dapat ditentukan dengan aturan kosinus segitiga.

s_AC² = s_AB² + s_BC² − 2 . s_AB . s_BC . cos B
        = 200² + 400² − 2 × 200 × 400 cos 60°
        = 40.000 + 160.000 − 80.000
        = 120.000
 s_AC = 200√3

Jadi, jarak tempuh kapal dari pelabuhan C ke pelabuhan A adalah 200√3 mil (B).

Simak soal sejenis di Pembahasan Matematika IPA UN 2017 No. 25
Perdalam materi ini di Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus.

Soal No. 22 tentang Dimensi Tiga (jarak titik ke garis)

Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak dari titik E ke garis BD adalah ...

A.   8√6 cm
B.   8√3 cm
C.   8√2 cm
D.   4√6 cm
E.   4√3 cm

Pembahasan

Perhatikan gambar kubus ABCD.EFGH berikut ini!

AC adalah diagonal bidang, sedangkan AO adalah setengah diagonal AC.

AC = a√2
      = 8√2

AO = ½ AC
       = ½ × 8√2
       = 4√2

Jarak titik E ke garis BD adalah garis EO. Pandanglah segitiga AOE.

Jadi, jarak dari titik E ke garis BD adalah 4√6 cm (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga].

Soal No. 23 tentang Dimensi Tiga (sudut antara garis dan bidang)

Diketahui kubus ABCD.EFGH dengan AB = 16 cm. Nilai sinus sudut antara garis AH dengan bidang BDHF adalah ....

A.   ½
B.   ⅓√3
C.   ½√2
D.   ½√3
E.   ⅓√6

Pembahasan

Perhatikan terbentuknya sudut antara garis AH dan bidang BDHF berikut ini!

Garis AH dan bidang BDHF bertemu di titik H. Dari titik H ini ditarik garis pertolongan hingga terbentuk sudut α.

Garis AH adalah diagonal bidang.

AH = a√2
       = 16√2

Sedangkan garis HB adalah diagonal ruang.

HB = a√3
      = 16√3

Cara I: Aturan Kosinus Segitiga

Pandanglah segitiga ABH! Sudut α dapat dicari dengan menggunakan aturan kosinus.

Jika masing-masing suku ruas kanan dibagi dengan 16² maka diperoleh:

Sayang sekali pertanyaannya sin α. Sabar sedikit, ya. Tinggal satu langkah lagi. Kita buat perbandingan trigonometri dengan memanfaatkan sifat segitiga siku-siku.

Nilai y pada segitiga siku-siku di atas adalah:

Dengan demikian, nilai dari sin α adalah:

Cara II: Segitiga Siku-siku

Jika Anda jeli, segitiga ABH adalah segitiga siku-siku di A.

Dengan demikian, nilai sin α adalah:

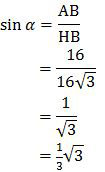
Jadi, nilai sinus sudut antara garis AH dengan bidang BDHF adalah ⅓√3 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga].

Soal No. 24 tentang Transformasi Geometri

Persamaan bayang kurva y = 3x² + 2x − 1 oleh pencerminan terhadap sumbu x yang dilanjutkan dengan pencerminan terhadap sumbu y adalah ....

A.   y = −3x² − 2x − 1
B.   y = −3x² − 2x + 1  y = −3x² + 2x + 1
C.   y = −3x² + 2x − 1
D.   y = 3x² + 2x + 1
E.   y = 3x² − 2x + 1

Pembahasan

Mencerminkan terhadap sumbu x dilanjutkan dengan mencerminkan terhadap sumbu y sama saja dengan mencerminkan terhadap pangkal koordinat atau memutar 180°. Sehingga bayangan dan benda akan saling bertolak belakang. Secara matematis dapat dinotasikan:

(x, y) → (−x, −y)

Sehingga diperoleh:

x' = −x   atau   x = −x'  ... (1)
y' = −y   atau   y = −y'  ... (2)

Persamaan bayangan kurva y diperoleh dengan cara substitusi persamaan (1) dan (2) pada kurva y.

kurva      :    y = 3x² + 2x − 1
bayangan: −y' = 3(−x')² + 2(−x') − 1
                        = 3(x')² − 2x' − 1
                     y' = −3(x')² + 2x' + 1

Jadi, persamaan bayangan kurva tersebut adalah y = −3x² + 2x + 1 (C B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri.

Soal No. 25 tentang Lingkaran

Salah satu persamaan garis singgung lingkaran x² + y² + 2x − 4y − 15 = 0 yang sejajar dengan garis 2x + y + 3 = 0 adalah ....

A.   2x + y + 10 = 0
B.   2x + y + 6 = 0
C.   2x + y + 4 = 0 
D.   2x + y − 6 = 0
E.   2x + y − 8 = 0

Pembahasan

Persamaan garis singgung lingkaran yang sejajar atau tegak lurus suatu garis dirumuskan sebagai:

dengan (h, k) adalah pusat lingkaran, r adalah jari-jari lingkaran, dan m adalah gradien garis singgung.

Kita tentukan dulu pusat dan jari-jari lingkaran dengan cara membandingkan dengan bentuk umumnya.

x² + y² + Ax + By + C = 0
x² + y² + 2x − 4y − 15 = 0

Dengan membandingkan bentuk umumnya diperoleh:

A = 2
B = −4
C = −15

Adapun pusat dan jari-jari lingkaran dirumuskan:

pusat: (−½A, −½B)
           (−½×2, −½×(−4))
           (−1, 2)

jari-jari:

Garis singgung lingkaran sejajar dengan garis 2x + y + 3 = 0, berarti gradien garis singgung sama dengan gradien garis tersebut.

Gradien garis ax + by + c = 0 dirumuskan:

m = −a/b

Sehingga gradien garis 2x + y + 3 = 0 adalah:

m = −2/1
    = −2

Dengan demikian, persamaan garis singgung lingkaran tersebut adalah:

Sekarang tinggal menguraikan nilai plus dan minus pada persamaan tersebut

y = −2x + 10
2x + y −10 = 0

dan

y = −2x − 10
2x + y +10 = 0

Jadi, salah satu persamaan garis singgung lingkaran adalah 2x + y + 10 = 0 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.

Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.