Pembahasan Matematika IPA UN 2016 No. 16 - 20

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPA nomor 16 sampai dengan nomor 20 tentang:

• penerapan barisan aritmetika, 
• deret geometri, 
• persamaan trigonometri, 
• grafik fungsi trigonometri, dan 
• perbandingan trigonometri.

Soal No. 16 tentang Penerapan Barisan Aritmetika

Aturan main:

Dalam kotak tersedia 10 bendera dan harus dipindahkan ke dalam botol yang tersedia satu demi satu (tidak sekaligus). Semua peserta lomba mulai bergerak (start) dari botol no. 10 untuk mengambil bendera dalam kotak. Jarak tempuh yang dilalui peserta lomba adalah ....

A.   164 meter
B.   880 meter
C.   920 meter
D.   1.000 meter
E.   1.840 meter

Pembahasan

Untuk mempermudah analisis, kita hitung jarak tempuh dari kotak bendera. Misalkan U_n adalah jarak tempuh dari kotak bendera ke botol n.

U₁ = 10
U₂ = 10 + 8
U₃ = 10 + 2×8
U₄ = 10 + 3×8
⋮
U₁₀ = 10 + 9×8
       = 82

Jarak tempuh tersebut membentuk barisan aritmetika dengan:

a = 10
b = 8
n = 10

Jumlah U₁ + U₂ + U₃ + ...+ U₁₀,  dalam deret aritmetika dikenal dengan S_n yang dirumuskan:

 S_n = ½ n (a + U_n)
S₁₀ = ½ ×10 (U₁ + U₁₀)
      = 5 (10 + 82)
      = 5 × 92
      = 460

Sementara itu, peserta lomba menempuh jarak dari kotak bendera ke botol 1 kemudian kembali ke kotak bendera (2×U₁), selanjutnya menuju botol 2 dan kembali lagi ke kotak bendera (2×U₂), dan seterusnya hingga botol 10.

Saat sampai di botol 10, peserta tidak kembali ke kotak bendera lagi. Tetapi ingat, awal start dimulai dari botol 10 ke kotak bendera (2×U₁₀).

Dengan demikian, jarak seluruh lintasan peserta lomba adalah 2 kali S₁₀.

jarak tempuh = 2 × S₁₀ 
                     = 2 × 460
                     = 920

Jadi, jarak tempuh yang dilalui peserta lomba adalah 920 meter (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 17 tentang Deret Geometri

Seorang pedagang pada bulan pertama menabung sebesar Rp20.000,00. Ternyata usahanya sukses sehingga tiap bulan ia menabung 1½ kali tabungan bulan sebelumnya. Besar uang yang ditabung pedagang tersebut pada bulan keempat adalah ....

A.   Rp151.875,00
B.   Rp160.000,00
C.   Rp162.500,00
D.   Rp180.000,00
E.   Rp196.000,00

Pembahasan

Soal di atas adalah penerapan deret geometri dengan:

a = 20.000
r = 1½ = 3/2
n = 4

Jumlah uang yang ditabung selama 4 bulan (S₄) adalah:

 
Jadi, besar uang yang ditabung pedagang tersebut pada bulan keempat adalah Rp162.500,00 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 18 tentang Persamaan Trigonometri

Himpunan penyelesaian dari persamaan trigonometri cos 2x + sin x = 0 untuk 0° < x < 360° adalah ....

A.   {60°, 120°, 150°}
B.   {60°, 150°, 300°}
C.   {90°, 210°, 300°}
D.   {90°, 210°, 330°}
E.   {120°, 250°, 330°}

Pembahasan

Langkah pertama adalah mengubah bentuk cos 2x menjadi:

cos 2x = 1 − 2 sin² x

Sehingga persamaan trigonometri tersebut menjadi:

            cos 2x + sin x = 0
⇔ 1 − 2 sin² x + sin x = 0
⇔ 2 sin² x − sin x − 1 = 0

Persamaan trigonometri di atas berbentuk persamaan kuadrat sehingga dapat difaktorkan menjadi:

(2 sin x + 1)(sin x − 1) = 0
sin x = −½  atau sin x = 1

Sin x yang bernilai negatif terjadi pada kuadran III dan kuadran IV.

     sin x = −½

K.III   x = 180° + 30°
              = 210°

K.IV   x = 360° − 30°
              = 330°

(angka 30° diperoleh dari sin x = ½) 

Sedangkan sin x = 1 hanya terjadi sekali dalam interval 0° < x < 360°.

sin x = 1
     x = 90°

Dengan demikian, himpunan penyelesaian persamaan trigonometri tersebut adalah:

{90°, 210°, 330°}

Jadi, himpunan penyelesaian dari persamaan trigonometri tersebut adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Trigonometri.

Soal No. 19 tentang Grafik Fungsi Trigonometri

Persamaan grafik fungsi trigonometri berikut adalah ....

A.   y = cos (2x − 30°)
B.   y = sin (2x + 30°)
C.   y = −cos (2x − 30°)
D.   y = −sin (2x − 30°)
E.   y = −cos (2x + 30°)

Pembahasan

Grafik trigonometri pada soal di atas bisa merupakan grafik sinus maupun kosinus, tergantung fase awalnya. Perhatikan grafik berikut ini!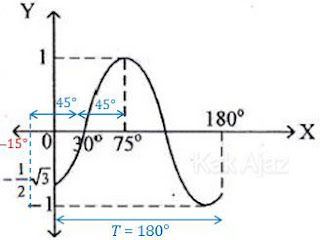

Pertama yang dapat kita ketahui dari grafik tersebut adalah amplitudo (A) dan periode (T).

A = ±1
T = 180° = π

Periode dapat digunakan untuk menentukan bilangan gelombang (k).

k = 2π/T
   = 2π/π
   = 2

Anggap saja grafik tersebut adalah grafik sinus, maka fase awalnya θ_o = 30° dan amplitudonya adalah A = 1. Persamaan grafik adalah:

y = A sin k(x − θ_o)
  = 1 sin 2(x − 30°)
  = sin (2x − 60°)

Ternyata persamaan ini tidak ada pada pilihan jawaban. Berarti persamaan trigonometri yang dimaksud adalah persamaan kosinus.

Fase awal persamaan kosinus pada grafik di atas adalah θ_o = −15° atau θ_o = 75°. Untuk fase awal 75° sepertinya tidak mungkin karena tidak ada opsi jawaban yang menunjukkan fase awal 75° atau kelipatannya. Jadi, sudah dapat dipastikan fase awalnya adalah −15°.

Pada fase awal −15°, grafiknya dimulai dari bawah kemudian bergerak ke atas. Hal ini berarti grafik kosinusnya adalah negatif atau amplitudonya A = −1.

y = A cos k(x − θ_o)
   = −1 cos 2(x − (−15°))
   =  −cos (2x + 30°)

Jadi, persamaan grafik fungsi trigonometri berikut adalah opsi (E).

Perdalam materi ini di Fungsi Trigonometri dan Grafknya [Soal UN dan Pembahasan].

Soal No. 20 tentang Perbandingan Trigonometri

Nilai dari

adalah ....

A.   −1
B.   −⅓√3
C.   ⅓√3
D.   √2
E.   √3

Pembahasan

Untuk menyelesaikan soal di atas harus hafal dua rumus berikut ini.

sin A + sin B   = 2 sin ½(A + B) cos ½(A − B)
cos A + cos B = 2 cos ½(A + B) cos ½(A − B)

Berdasarkan rumus di atas diperoleh:

sin 100° + sin 20° = 2 sin 60° cos 40°
cos 250° + cos 190° = 2 cos 220° cos 30°

Sehingga soal di atas menjadi:

Sudut 220° berada di kuadran III sehingga dapat disederhanakan menjadi:

cos 220° = cos (180° + 40°)
               = −cos 40°

Dengan demikian diperoleh:

Jadi, nilai perbandingan trigonometri tersebut adalah −1 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Perbandingan Trigonometri.

Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.