Pembahasan Matematika IPA UN 2016 No. 6 - 10

Pembahasan soal-soal Ujian Nasional (UN) tahun 2016 bidang studi Matematika SMA-IPA nomor 6 sampai dengan nomor 10 tentang:

• fungsi kuadrat, 
• sistem persamaan linear, 
• program linear, 
• fungsi komposisi, dan 
• invers fungsi.

Soal No. 6 tentang Fungsi Kuadrat

Diketahui fungsi f(x) = (a + 1)x² − 2ax + (a − 2) definit negatif. Nilai a yang memenuhi adalah ....

A.   a < 2
B.   a > −2
C.   a < −1
D.   a < −2
E.   a > 1

Pembahasan

Fungsi f(x) dikatakan definit negatif apabila f(x) selalu bernilai negatif untuk semua nilai x. Hal ini terjadi apabila kurva f(x) berada di bawah sumbu x.

Syarat agar fungsi kuadrat f(x) definit negatif adalah kurva parabola terbuka ke bawah dan tidak memotong ataupun menyinggung sumbu x.

Kurva parabola akan terbuka ke bawah apabila koefisien kuadratnya bernilai negatif. 

a + 1 < 0
      a < −1    ... (1)

Sedangkan syarat agar kurva parabola tidak memotong maupun menyinggung sumbu x adalah diskriminan fungsi f(x) harus bernilai negatif.

                                   D < 0
                        b² − 4ac < 0
(−2a)² − 4(a + 1)(a − 2) < 0
        4a² − 4(a² − a − 2) < 0
        4a² − 4a² + 4a + 8 < 0
                            4a + 8 < 0
                                  4a < −8
                                    a < −2 ... (2)

Selanjutnya kita buat garis bilangan untuk pertidaksamaan (1) dan (2).

Berdasarkan garis bilangan tersebut, nilai a yang memenuhi adalah: 

a < −2

Jadi, agar f(x) definit positif maka rentang nilai a adalah a < −2 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Fungsi Kuadrat.

Soal No. 7 tentang Sistem Persamaan Linear

Ibu Abdaya berbelanja di swalayan membeli 5 kg bakso rasa daging sapi dan 4 kg bakso rasa ikan dengan harga Rp550.000,00. Secara bersamaan di swalayan tersebut Ibu Rita Zahara membeli 4 kg bakso rasa daging sapi dan 5 kg bakso rasa ikan dengan harga Rp530.000,00. Di swalayan yang sama Ibu Emi membeli 2 kg bakso rasa daging sapi dan 3 kg bakso rasa ikan. Uang yang harus dibayar Ibu Emi adalah ....

A.   Rp240.000,00
B.   Rp280.000,00
C.   Rp285.000,00
D.   Rp290.000,00
E.   Rp310.000,00

Pembahasan

Misalkan:

x : bakso rasa daging sapi
y : bakso rasa ikan

Model matematika untuk soal di atas adalah:

Abdaya : 5x + 4y = 550.000 ...(1)
Rita       : 4x + 5y = 530.000 ...(2)
Emi       : 2x + 3y = ?

Mari kita eliminasi persamaan (1) dan (2). Persamaan (1) kita kalikan 5 sedangkan persamaan (2) kita kalikan 4 untuk mendapatkan koefisien y yang sama.

25x + 20y = 2.750.000
16x + 20y = 2.120.000
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
            9x = 630.000
              x = 70.000

Selanjutnya kita substitusikan x = 70.000 ke persamaan (1).

           5x + 4y = 550.000
5×70.000 + 4y = 550.000
  350.000 + 4y = 550.000
                   4y = 550.000 − 350.000
                        = 200.000
                     y = 50.000

Dengan demikian, harga 2 kg bakso rasa daging sapi dan 3 kg bakso rasa ikan adalah:

2x + 3y = 2×70.000 + 3×50.000
             = 140.000 + 150.000
             = 290.000

Jadi, uang yang harus dibayar Ibu Emi sebesar Rp290.000,00 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sistem Persamaan dan Pertidaksamaan Linear.

Soal No. 8 tentang Program Linear

Seorang penjahit memiliki persediaan 20 m kain polos dan 20 m lain bergaris untuk membuat 2 jenis pakaian. Pakaian model I memerlukan 1 m kain polos dan 3 m kain bergaris. Pakaian model II memerlukan 2 m kain polos dan 1 m kain bergaris. Pakaian model I dijual dengan harga Rp150.000,00 per potong dan pakaian model II dijual dengan harga Rp100.000,00 per potong. Penghasilan maksimum yang dapat diperoleh penjahit tersebut adalah ....

A.   Rp1.400.000,00
B.   Rp1.600.000,00
C.   Rp1.800.000,00
D.   Rp1.900.000,00
E.   Rp2.000.000,00

Pembahasan

Tabel bantuan untuk soal di atas adalah:

	Model I (x)	Model II (y)
Kain polos	1	2	20
Kain bergaris	3	1	20
Harga jual	150.000	100.000

Model matematika berdasarkan tabel bantuan di atas adalah:

x + 2y = 20  ... (1)
3x + y = 20  ... (2)
z = 150.000x + 100.000y

Eliminasi persamaan (2) dan (1). Persamaan (2) dikalikan 2 terlebih dahulu.

6x + 2y = 40
  x + 2y = 20
⎯⎯⎯⎯⎯⎯⎯  −
         5x = 20
           x = 4

Substitusi x = 4 ke persamaan (1) diperoleh:

x + 2y = 20
4 + 2y = 20
      2y = 16
        y = 8

Dengan demikian nilai z adalah:

z = 150.000x + 100.000y
  = 150.000 × 4 + 100.000 × 8
  = 600.000 + 800.000
  = 1.400.000

Jadi, penghasilan maksimum yang dapat diperoleh penjahit tersebut adalah Rp1.400.000,00 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Program Linear.

Soal No. 9 tentang Fungsi Komposisi

Diketahui fungsi f(x) = x² + 2x dan g(x) = x − 3. Fungsi komposisi (f ∘ g)(x) adalah ....

A.   (f ∘ g)(x) = x² − 4x + 6
B.   (f ∘ g)(x) = x² − 4x + 3
C.   (f ∘ g)(x) = x² + 2x + 6
D.   (f ∘ g)(x) = x² + 2x − 6
E.   (f ∘ g)(x) = x² + 3x − 3

Pembahasan

Jika fungsi f(x) diartikan sebagai fungsi f yang dinyatakan dalam x maka fungsi komposisi (f ∘ g)(x) berarti fungsi f yang dinyatakan dalam g(x).

        f(x) = x² + 2x
(f ∘ g)(x) = g²(x) + 2g(x)
               = (x − 3)² + 2(x − 3)
               = x² − 6x + 9 + 2x − 6
               = x² − 4x + 3

Jadi, fungsi komposisi (f ∘ g)(x) adalah x² − 4x + 3 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi.

Soal No. 10 tentang Invers Fungsi

Diketahui f : R → R dan g : R → R didefinisikan dengan f(x) = (3x + 1)/(x − 5), x ≠ 5 dan g(x) = x − 3. Invers dari (f ∘ g)(x) adalah ....

Pembahasan

Kita tentukan dulu fungsi komposisi (f ∘ g)(x).

Untuk menentukan invers dari fungsi komposisi tersebut, perhatikan konsep berikut ini!

Berdasarkan konsep di atas maka:

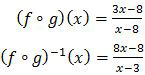
Jadi, invers dari (f ∘ g)(x) adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi.

Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.