Soal tentang Aturan Sinus dan Kosinus UN 2011
Dalam suatu lingkaran yang berjari-jari 8 cm dibuat segi-8 beraturan. Panjang sisi segi-8 tersebut adalah ….
A. √(128 − 64√3) cm
B. √(128 − 64√2) cm
C. √(128 − 16√2) cm
D. √(128 + 16√2) cm
E. √(128+16√3) cm
A. √(128 − 64√3) cm
B. √(128 − 64√2) cm
C. √(128 − 16√2) cm
D. √(128 + 16√2) cm
E. √(128+16√3) cm
Pembahasan
Perhatikan gambar segi-8 berikut ini!
Sisi segi-8 tersebut adalah s. Di dalam Segi-8 terbentuk 8 segitiga sama kaki yang masing-masing mempunyai sudut puncak α.
Besar sudut α dapat dicari dengan rumus:
α = 360° : n, n = jumlah segi suatu bangun
= 360° : 8
= 45°
Sekarang perhatikan segitiga ABO! Panjang sisi s pada segitiga tersebut dapat dicari dengan aturan kosinus berikut ini.
s2 = OA2 + OB2 − 2OA ∙ OB ∙ cos α
= 82 + 82 − 2 ∙ 8 ∙ 8 ∙ cos 45°
= 64 + 64 − 128 ∙ ½√2
= 128 − 64√2
s = √(128 − 64√2)
Jadi, panjang sisi segi-8 tersebut adalah √(128 − 64√2) cm (B).
Soal tentang Aturan Sinus dan Kosinus UN 2013
Keliling segi-12 beraturan yang jari-jari lingkaran luarnya r cm adalah ….
A. 2r√(2 − √3) cm
B. 6r√(2 − √3) cm
C. 12r√(2 − √3) cm
D. 6r√(2 + √3) cm
E. 22r√(2 + √3) cm
A. 2r√(2 − √3) cm
B. 6r√(2 − √3) cm
C. 12r√(2 − √3) cm
D. 6r√(2 + √3) cm
E. 22r√(2 + √3) cm

Pembahasan
Dalam segi-12 terbentuk 12 segitiga sama kaki yang masing-masing mempunyai sudut puncak:α = 360° : 12
= 30°
Perhatikan gambar segitiga yang terdapat dalam segi-12 berikut ini!

Panjang sisi s dapat ditentukan aturan kosinus berikut ini.
s2 = r2 + r2 − 2 r r cos 30°
= 2r2 − 2r2 ∙ ½√3
= 2r2 − r2√3
= r2 (2 − √3)
s = r√(2 − √3)
Dengan demikian, keliling segi-12 tersebut adalah:
K = 12s
= 12r√(2 − √3)
Jadi, keliling segi-12 beraturan yang jari-jari lingkaran luarnya r cm adalah 12r√(2 − √3) cm (C).
Soal tentang Aturan Sinus dan Kosinus UN 2012
Luas segi-12 beraturan adalah 192 cm2. Keliling segi-12 beraturan tersebut adalah ….
A. 96√(2 + √3) cm
B. 96√(2 − √3) cm
C. 8√(2 + √3) cm
D. 8√(2 − √3) cm
E. √(128 − √3) cm
A. 96√(2 + √3) cm
B. 96√(2 − √3) cm
C. 8√(2 + √3) cm
D. 8√(2 − √3) cm
E. √(128 − √3) cm
Pembahasan
Di dalam segi-12 terdapat 12 segitiga sama kaki. Sehingga luas tiap segitiga tersebut adalah:L∆ = (L. segi-12) : 12
= 192 : 12
=16
Sedangkan sudut puncak segitiga tersebut adalah:
α = 360° : 12
= 30°
Perhatikan rumus segitiga berikut!

Dengan memanfaatkan rumus di atas, diperoleh:
L∆ = ½ r2 sin 30°
16 = ½ . r2 ∙ ½
r2 = 64
r = 8
Berdasarkan jawaban soal sebelumnya, bahwa keliling segi-12 yang berjari-jari r adalah:
K = 12r√(2 − √3)
Dengan memasukkan r = 8 diperoleh:
K = 12 × 8√(2 − √3)
= 96√(2 − √3)
Jadi, keliling segi-12 beraturan tersebut adalah 96√(2 − √3) cm (B).
Soal tentang Aturan Sinus dan Kosinus UN 2014
Diketahui segiempat ABCD seperti tampak pada gambar.
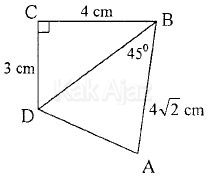
Panjang AD adalah ….
A. √17 cm
B. 5 cm
C. 6 cm
D. √45 cm
E. 7 cm

Panjang AD adalah ….
A. √17 cm
B. 5 cm
C. 6 cm
D. √45 cm
E. 7 cm
Pembahasan
Perhatikan segitiga BCD dalam segiempat ABCD pada soal di atas. Segitiga BCD adalah segitiga siku-siku sehingga panjang BD dapat dicari dengan teorema Pythagoras.BD = √(BC2 + CD2 )
= √(42 + 32 )
= 5
Sekarang perhatikan segitiga ABD di bawah ini!

Karena panjang BD sudah diketahui maka panjang AD dapat dicari dengan aturan kosinus.
AD2 = AB2 + BD2 − 2AB ∙ BD ∙ cos 45°
= (4√2)2 + 52 − 2 ∙ 4√2 ∙ 5 ∙ ½√2
= 32 + 25 − 40
= 17
AD = √17
Jadi, panjang AD pada segiempat ABCD tersebut adalah √17 cm (A).
Soal tentang Aturan Sinus dan Kosinus UN 2015
Perhatikan gambar!
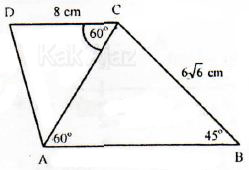
Panjang AD adalah ….
A. 2√21 cm
B. 2√19 cm
C. 2√13 cm
D. 4√7 cm
E. 4√10 cm

Panjang AD adalah ….
A. 2√21 cm
B. 2√19 cm
C. 2√13 cm
D. 4√7 cm
E. 4√10 cm
Pembahasan
Perhatikan segitiga ABC di bawah ini yang diambil dari segiempat ABCD pada soal di atas.
Pada segitiga di atas diketahui nilai dari satu sisi dan dua sudut. Sehingga kita dapat memanfaatkan rumus sinus berikut ini.

Sekarang perhatikan segitiga ACD!
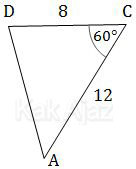
Pada segitiga di atas, diketahui nilai dari satu sudut dan sua sisi sehingga bisa diselesaikan dengan aturan kosinus.
AD2 = AC2 + CD2 − 2AC ∙ CD ∙ cos 60°
= 122 + 82 − 2 ∙ 12 ∙ 8 ∙ ½
= 144+ 64 − 96
= 112
AD = √112
= √(16×7)
= 4√7
Jadi, panjang AD pada segiempat ABCD di atas adalah 4√7 cm (D).
Pembahasan soal Aturan Sinus dan Kosinus yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 25
Pembahasan Matematika IPA UN 2014 No. 24
Pembahasan Matematika IPA UN 2015 No. 26
Pembahasan Matematika IPA UN 2016 No. 21
Pembahasan Matematika IPA UN 2017 No. 25
Pembahasan Matematika IPA UN 2019 No. 26
Pembahasan Matematika IPA UN 2019 No. 38
Pembahasan Matematika IPA UN 2019 (2) No. 24
Pembahasan Matematika IPA UN 2019 (2) No. 38
Simak juga,
Pembahasan Matematika IPA UN: Persamaan Trigonometri.
Fungsi Trigonometri dan Grafiknya [Soal UN dan Pembahasan]
Pembahasan Matematika IPA UN: Perbandingan Trigonometri
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan