Pembahasan Matematika IPA UN 2019 No. 26 - 30

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 26 sampai dengan nomor 30 tentang:

• aturan sinus dan kosinus, 
• transformasi geometri, 
• statistika [penyajian data], 
• statistika [ukuran pemusatan], dan 
• statistika [ukuran letak].

Soal No. 26 tentang Aturan Sinus dan Kosinus

Sebuah kapal pesiar berlayar dari pelabuhan P menuju pelabuhan Q berjarak 200 km dengan arah jurusan tiga angka 080°. Kemudian dari pelabuhan Q berlayar lagi menuju pelabuhan R berjarak 300 km dengan arah jurusan tiga angka 200°. Jarak pelabuhan P ke pelabuhan R adalah ….

A.   100√7 km
B.   125√7 km
C.   150√7 km
D.   175√7 km
E.   200√7 km

Pembahasan

Perhatikan gambar berikut ini!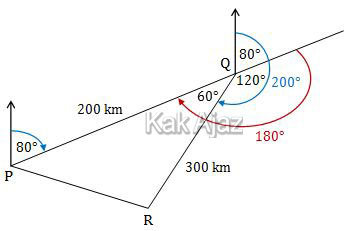

Berdasarkan gambar di atas, jarak PR dapat dicari dengan aturan kosinus berikut ini.

PR² = PQ² + QR² − 2PQ ∙ QR cos ⁡Q
        = 200² + 300² − 2 ∙ 200 ∙ 300 cos⁡ 60°
        = 40000 + 90000 − 120000 ∙ 0,5
        = 70000
  PR = √70000
        = 100√7

Jadi, jarak pelabuhan P le pelabuhan R adalah 100√7 km (A).

Perdalam materi ini di Pembahasan Matematika UN: Aturan Sinus dan Kosinus.

Soal No. 27 tentang Transformasi Geometri

Persamaan bayangan garis 2y + 4x − 1 = 0 jika didilatasikan dengan menggunakan faktor skala 2 dengan titik pusat (0, 0) dilanjutkan rotasi sejauh 90° berlawanan arah jarum jam dengan titik pusat (0, 0) adalah ….

A.   y − x − 3 = 0
B.   −x − y + 3 = 0
C.    x − y − 3 = 0
D.   2x - y − 1 = 0
E.   x − 2y + 1 = 0

Pembahasan

Misal T₁ adalah dilatasi dengan faktor skala k = 2, matriks transformasinya adalah: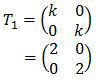

Sedangkan T₂ adalah rotasi 90° berlawanan arah jarum (+90°), matriks transformasinya adalah:

Komposisi dari transformasi T₁ dilanjutkan T₂ dirumuskan:

Sedangkan persamaan transformasinya dirumuskan:

Sehingga diperoleh:

y = −1/2 x'
x = 1/2 y'

Bayangan garis dapat dicari dengan melakukan substitusi kedua persamaan di atas.

                      2y + 4x − 1 = 0
2(−1/2 x') + 4 ∙ 1/2 y' − 1 = 0
                    −x' + 2y' − 1 = 0
                      x' − 2y' + 1 = 0

Jadi, persamaan bayangan garis tersebut adalah x − 2y + 1 = 0 (E).

Perdalam materi ini di Pembahasan Matematika UN: Transformasi Geometri.

Soal No. 28 tentang Statistika [Penyajian Data]

Diagram batang berikut menunjukkan produksi pakaian yang dikelola Bu Rahmi selama tahun 2017 dari bulan Januari sampai bulan Desember.

Peningkatan tertinggi jumlah produksi pakaian Bu Rahmi terjadi pada bulan ….

A.   April
B.   Juni
C.   Juli
D.   September
E.   November

Pembahasan

Peningkatan tertinggi terjadi bila terdapat selisih yang paling besar terhadap bulan sebelumnya. Mari kita periksa setiap opsi jawaban.

A.   April : 151 – 112 = 39
B.   Juni : 81 – 18 = 63
C.   Juli : 133 – 81 = 52
D.   September : 166 – 150 = 16
E.   November : 153 – 87 = 66

Jadi, peningkatan tertinggi jumlah produksi pakaian Bu Rahmi terjadi pada bulan November (E).

Perdalam materi ini di Pembahasan Matematika UN: Statistika.

Soal No. 29 tentang Statistika [Ukuran Pemusatan]

Data di bawah ini adalah data skor hasil ulangan matematika kelas XII IPA suatu SMA.

Skor	Frekuensi
21 – 25	5
26 – 30	8
31 – 35	12
36 – 40	18
41 – 45	16
46 – 50	5

Modus data pada tabel adalah ….

A.   36,75
B.   37,25
C.   38,00
D.   38,50
E.   39,25

Pembahasan

Modus adalah nilai yang sering muncul atau nilai dengan frekuensi tertinggi.
Perhatikan penentuan besaran-besaran modus berikut ini!

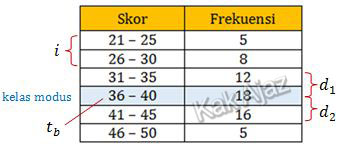
Berdasarkan keterangan di atas diperoleh:

 t_b = 36 − 0,5 = 35,5
d₁ = 18 − 12 = 6
d₂ = 18 − 16 = 2
  i = 26 − 21 = 5

Nah, mari kita hitung modus data tersebut!

Jadi, modus data pada tabel di atas adalah 39,25 (E).

Perdalam materi ini di Pembahasan Matematika UN: Statistika.

Soal No. 30 tentang Statistika [Ukuran Letak]

Perhatikan gambar di bawah ini!

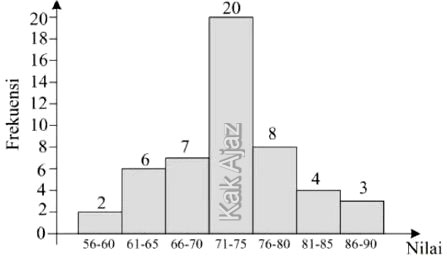
Kuartil ke-2 (Q₂) dari data pada histogram di tersebut adalah ….

A.   71,5
B.   72
C.   72,5
D.   73
E.   73,5

Pembahasan

Kita hitung dulu jumlah datanya.

      N = 2 + 6 + 7 + 20 + 8 + 4 + 3
          = 50
2/4 N = 25

Berarti kuartil ke-2 terletak pada data ke-25. Perhatikan gambar berikut ini!

Besaran-besaran yang dpt diperoleh dari data tersebut adalah:

t_b = 71 − 0,5 = 70,5
f_k = 2 + 6 + 7 = 15
  f = 20
  i = 65 − 60 = 5

Kuartil ke-2 sebenarnya sama dengan median. Namun kita tetap menggunakan rumus kuartil saja.

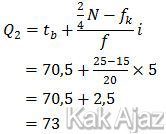
Jadi, kuartil ke-2 (Q_2 ) dari data pada histogram di tersebut adalah 73 (D).

Perdalam materi ini di Pembahasan Matematika UN: Statistika.

Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.