Pembahasan Matematika IPA UN 2018 No. 21 - 25

Pembahasan soal-soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPA nomor 21 sampai dengan nomor 25 tentang:

• integral tentu, 
• trigonometri, 
• aplikasi trigonometri, 
• segitiga trigonometri, dan 
• dimensi tiga [jarak titik ke titik]

Soal No. 21 tentang Integral Tentu

Diketahui

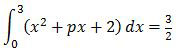
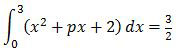
Nilai p yang memenuhi adalah ….

A.   −26
B.   −13
C.   −3
D.   3
E.   13

Pembahasan

Integral tentu atau integral batas di atas dapat diselesaikan sebagai berikut: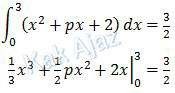

Batas integrasi yang dimasukkan cukup x = 3 saja karena batas x = 0 akan menghasilkan nol.

1/3 ∙ 3³ + 1/2 ∙ p ∙ 3² + 2 ∙ 3 = 3/2
                        9 + 9/2 p + 6 = 3/2
                        18 + 9p + 12 = 3    [dikalikan 2]
                                         9p = −27
                                           p = −3

Jadi, nilai dari integral tentu tersebut adalah −3 (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Integral Fungsi Aljabar

Soal No. 22 tentang Trigonometri

Diketahui segitiga ABC siku-siku di B dan sin⁡ R = 8/17 (P dan R sudut lancip). Nilai dari (1 − cos ⁡R)(1 + sin ⁡P) adalah ….

A.   17/8
B.   17/15
C.   64/289
D.   −64/289
E.   −225/289

Pembahasan

Mungkin yang dimaksud soal adalah segitiga PQR siku-siku di Q.

Berdasarkan gambar di atas diperoleh:

cos ⁡R = 15/17 dan sin ⁡P = 15/17

Dengan demikian,

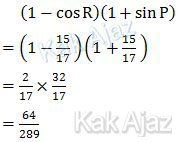
Jadi, nilai dari (1 − cos ⁡R)(1 + sin ⁡P) adalah 64/289 (C).

Soal No. 23 tentang Aplikasi Trigonometri

Sisno diminta mengukur tinggi tiang bendera menggunakan klinometer.

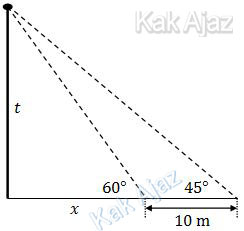
Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut 60°. Kemudian ia bergerak menjauhi tiang bendera sejauh 10 m dan terlihat pada klinometer sudut 45°. Tinggi tang bendera adalah ….

A.   (15 + 10√3) m
B.   (15 + 5√3) m
C.   (15 − 5√3) m
D.   (15 − 10√3) m
E.   (5 + 10√3) m

Pembahasan

Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut 60°.

tan⁡ 60° = t/x
       √3 = t/x
          t = √3 x … (1)

Kemudian ia bergerak menjauhi tiang bendera sejauh 10 m dan terlihat pada klinometer sudut 45°.

tan⁡ 45° = t/(x + 10)
         1 = t/(x + 10)
          t = x + 10 … (2)

Persamaan (1) dan (2) kita samakan menjadi:

        √3 x = x + 10
  √3 x − x = 10
(√3 − 1)x = 10
             x = 10/(√3 − 1)

Nilai x dalam bentuk akar ini kita sederhanakan dengan mengalikan bilangan sekawan.

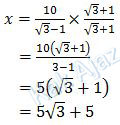
Tinggi tiang bendera bisa kita cari dengan melakukan substitusi nilai x di atas ke persamaan (1) atau (2). Kak Ajaz pakai persamaan (1) saja ya.

t = x + 10
  = 5√3 + 5 + 10
  = 15 + 5√3

Jadi, tiang bendera tersebut adalah (15 + 5√3) m (B).

Soal No. 24 tentang Segitiga Trigonometri

Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60° dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter maka luas taman tersebut adalah ….

A.   72 m²
B.   72√2 m²
C.   72√3 m²
D.   144 m²
E.   144√3 m²

Pembahasan

Luas segitiga dengan sudut apit α dan sisi apit a dan b adalah:

L = 1/2 ab sin ⁡α
   = 1/2 × 18 × 16 × sin 60°
   = 1/2 × 18 × 16 × 1/2 √3
   = 9 × 8√3
   = 72√3

Jadi, luas taman segitiga tersebut adalah 72√3 m² (C).

Soal No. 25 tentang Dimensi Tiga [jarak titik ke titik]

Kamar Andi berbentuk balok dengan panjang 4 m, lebar 3 m, dan tinggi 3 m. Andi memasang lampu di tengah-tengah rusuk tegak salah satu dinding kamarnya. Jarak sinar lampu terjauh di kamar Andi adalah ….

A.   1/2 √109 m
B.   1/2 √106 m
C.   1/2 √91 m
D.   1/4 √109 m
E.   1/4 √106 m

Pembahasan

Gambar ilustrasi kamar Andi adalah sebagai berikut: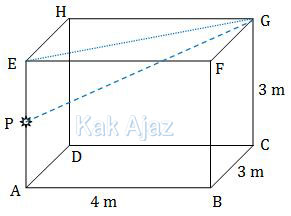

Jarak sinar lampu terjauh di kamar Andi adalah PC atau PG. Kak Ajaz ambil PG saja.
EG adalah diagonal atap kamar Andi.

EG = √(4² + 3²)
      = 5

Sedangkan panjang PE sama dengan setengah rusuk tegak (setengah tinggi dinding).

PE = 1/2 AE
      = 1/2 × 3
      = 3/2

Segitiga PGE adalah segitiga siku-siku di E.

Dengan demikian, jarak PG adalah:

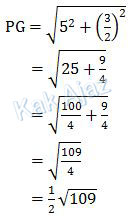
Jadi, jarak sinar lampu terjauh di kamar Andi adalah 1/2 √109 m (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang

Simak Pembahasan Soal Matematika IPA UN 2018 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.