- negasi pernyataan,
- ekuivalensi,
- penarikan kesimpulan,
- eksponen, dan
- bentuk akar.
Soal No. 1 tentang Negasi Pernyataan
Negasi dari pernyataan "Semua bilangan rasional adalah bilangan real dan prima" adalah ...
A. Tidak ada bilangan rasional adalah bilangan real dan prima.
B. Ada bilangan real adalah bilangan rasional atau prima.
C. Ada bilangan real yang bukan bilangan rasional dan prima.
D. Semua bilangan rasional bukan bilangan real atau bukan prima.
E. Ada bilangan rasional yang bukan bilangan real atau bukan prima.
A. Tidak ada bilangan rasional adalah bilangan real dan prima.
B. Ada bilangan real adalah bilangan rasional atau prima.
C. Ada bilangan real yang bukan bilangan rasional dan prima.
D. Semua bilangan rasional bukan bilangan real atau bukan prima.
E. Ada bilangan rasional yang bukan bilangan real atau bukan prima.
Pembahasan
Model matematika untuk pernyataan di atas adalah∀(p ∧ q)
∀ adalah kuantor universal yang mewakili kata 'setiap', 'semua', 'seluruh'. Ingkaran dari kuantor universal adalah kuantor khusus yang dilambangkan ∃ untuk mewakili kata 'sebagian', 'ada', 'beberapa'.
Jika pernyataan di atas dinegasikan maka akan menjadi
Hasil negasi pernyataan tersebut dibaca "Ada bilangan rasional yang bukan bilangan real atau bukan prima".
Jadi, ingkaran dari pernyataan tersebut yang tepat adalah opsi (E).
Soal No. 2 tentang Ekuivalensi
Pernyataan yang setara dengan ~r ⇒ (p ∨ ~q) adalah ....
A. (p ∧ ~q) ⇒ ~r
B. (~p ∧ q) ⇒ r
C. ~r ⇒ (p ∧ ~q)
D. ~r ⇒ (~p ∨ q)
E. r ⇒ (~p ∧ q)
A. (p ∧ ~q) ⇒ ~r
B. (~p ∧ q) ⇒ r
C. ~r ⇒ (p ∧ ~q)
D. ~r ⇒ (~p ∨ q)
E. r ⇒ (~p ∧ q)

Pembahasan
Pernyataan yang setara dengan implikasi adalah kontraposisinya.p ⇒ q ≡ ~q ⇒ ~p
Berdasarkan kesetaraan di atas diperoleh
~r ⇒ (p ∨ ~q) ≡ ~(p ∨ ~q) ⇒ ~(~r)
≡ (~p ∧ q) ⇒ r
Jadi, pernyataan yang setara adalah opsi (B).
Soal No. 3 tentang Penarikan Kesimpulan
Diketahui premis-premis:
A. Jika harga BBM naik maka harga tarif dasar listrik tidak naik.
B. Jika harga barang tidak naik maka harga BBM tidak naik.
C. Jika harga barang naik maka harga BBM naik.
D. Harga barang tidak naik tetapi harga BBM naik.
E. Harga tarif dasar listrik tidak naik maka harga BBM naik.
- Jika harga BBM naik maka tarif dasar listrik naik.
- Jika harga barang tidak naik maka tarif dasar listrik tidak naik.
A. Jika harga BBM naik maka harga tarif dasar listrik tidak naik.
B. Jika harga barang tidak naik maka harga BBM tidak naik.
C. Jika harga barang naik maka harga BBM naik.
D. Harga barang tidak naik tetapi harga BBM naik.
E. Harga tarif dasar listrik tidak naik maka harga BBM naik.
Pembahasan
Kita misalkan terlebih dahulup : harga BBM naik
q : tarif dasar listrik naik
r : harga barang naik
Premis-premis di atas menjadi
p ⇒ q
~r ⇒ ~q
Agar dapat ditarik kesimpulan, premis yang kedua kita ubah ke bentuk kontraposisinya.
~r ⇒ ~q ≡ q ⇒ r
Dengan demikian, kedua premis tersebut dapat kita tarik kesimpulan secara silogisme sebagai berikut:
p ⇒ q
q ⇒ r
————
∴ p ⇒ r
(Jika harga BBM naik maka harga barang naik)
Jawaban di atas tidak tersedia pada opsi jawaban. Kalau begitu, kita cari ekuivalensinya.
p ⇒ r ≡ ~r ⇒ ~p
(Jika harga barang tidak naik maka harga BBM tidak naik).
Jadi, kesimpulan dari kedua premis tersebut adalah opsi (B).
Soal No. 4 tentang Eksponen
Bentuk sederhana dari
%5E%7B-2%7D)
adalah ....
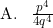
%5E%7B4%7D)
%5E%7B4%7D)
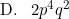
%5E%7B4%7D)
adalah ....
Pembahasan
Langkah pertama adalah mengubah pangkat di luar kurung, yaitu −2, menjadi pangkat positif. Caranya dengan membalik pecahan, pembilang jadi penyebut dan penyebut jadi pembilang.16 bisa langsung dibagi 8. Selanjutnya, kita lakukan pengurangan pangkat, pangkatnya p pada pembilang dikurangkan dengan pangkatnya p pada penyebut. Demikian juga dengan q.
(2p−1+3 q−4+2)2
= 4(p2 q−2)2
= 4(p q−1)4
= 4(p/q)4
Jadi, bentuk sederhana dari eksponen tersebut adalah opsi (C).
Soal No. 5 tentang Bentuk Akar
Bentuk sederhana dari √18 + 2√72 − √32 − √50 adalah ....
A. 4√2
B. 6√2
C. 10√2
D. 16√2
E. 20√2
A. 4√2
B. 6√2
C. 10√2
D. 16√2
E. 20√2
Pembahasan
Kita sederhanakan bentuk akar tersebut menjadi bentuk √2.√18 + 2√72 − √32 − √50
= √(9×2) + 2√(36×2) − √(16×2) − √(25×2)
= 3√2 + 12√2 − 4√2 − 5√2
= (3 + 12 − 4 − 5)√2
= 6√2
Jadi, bentuk sederhana dari bentuk akar tersebut adalah 6√2 (B).
Simak Pembahasan Soal Matematika IPS UN 2014 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

No comments:
Post a Comment
Maaf, komentar yang tidak berhubungan dengan konten, banyak mengandung singkatan kata, atau mengandung link aktif, tidak kami tayangkan.
Komentar Anda akan kami moderasi sebelum kami tayangkan. Centang 'Notify me' agar Anda mendapat pemberitahuan lewat email bahwa komentar Anda sudah ditayangkan