Pembahasan Matematika IPS UN 2014 No. 21

Pembahasan soal Matematika IPS Ujian Nasional tahun 2014 nomor 21 sampai dengan nomor 25 tentang:

kesamaan matriks,
determinan matriks,
invers matriks,
perkalian matriks, serta
barisan dan deret aritmetika.

Soal No. 21 tentang Kesamaan Matriks

Jika

$Kesamaan matriks$

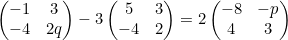
maka nilai dari 2p + q = ....

A.   12
B.   9
C.   6
D.   3
E.   −3

Pembahasan

Kita tidak perlu mengoperasikan keseluruhan komponen matriks. Cukup mengoperasikan komponen matriks yang mengandung variabel, yaitu komponen matriks yang terletak pada kanan-atas dan kanan-bawah.

Kita operasikan komponen matriks yang terletak pada kanan-atas.

3 − 3 . 3 = 2 (−p)
     3 − 9 = −2p
         −6 = −2p
            p = 3

Kemudian kita operasikan komponen matriks yang terletak pada kanan-bawah.

2q − 3 . 2 = 2 . 3
     2q − 6 = 6
           2q = 12
              q = 6

Nilai p dan q ini tinggal kita masukkan ke pertanyaan.

2p + q = 2 . 3 + 6
            = 6 + 6
            = 12

Jadi, nilai dari 2p + q adalah 12 (A).

Soal No. 22 tentang Determinan Matriks

Diketahui

$Matriks P, Q, dan R$

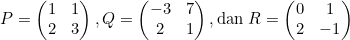
Determinan dari 2P − Q + R adalah ....

A.   16
B.   18
C.   24
D.   36
E.   38

Pembahasan

Langkah pertama kita tentukan nilai dari 2P − Q + R.

$Matriks 2P-Q+R$
                         $=\begin{pmatrix} 5 & -4\\ 4 & 4 \end{pmatrix}$

Setelah itu kita tentukan nilai determinannya dengan rumus yang sangat populer, yaitu ad − bc.

det (2P − Q + R) = 5 . 4 − (−4) . 4
                          = 20 + 16
                            = 36

Jadi, determinan dari 2P − Q + R adalah 36 (D).

Soal No. 23 tentang Invers matriks

Diketahui matriks

$A=\begin{pmatrix} 8 & 3\\ 5 & 2 \end{pmatrix}\textrm{dan }B=\begin{pmatrix} 6 & 4\\ 7 & 5 \end{pmatrix}$

Jika A + B = C, invers matriks C adalah ....

$\textrm{A. }\; \; \begin{pmatrix} -\frac{1}{2} & -\frac{1}{2}\\ -\frac{6}{7} & 1 \end{pmatrix}$
$\textrm{B. }\; \; \begin{pmatrix} -\frac{1}{2} & \frac{1}{2}\\ \frac{6}{7} & 1 \end{pmatrix}$
$\textrm{C. }\; \; \begin{pmatrix} \frac{1}{2} & \frac{1}{2}\\ \frac{6}{7} & -1 \end{pmatrix}$
$\textrm{D. }\; \; \begin{pmatrix} \frac{1}{2} & -\frac{1}{2}\\ \frac{6}{7} & 1 \end{pmatrix}$
$\textrm{E. }\; \; \begin{pmatrix} \frac{1}{2} & -\frac{1}{2}\\ -\frac{6}{7} & 1 \end{pmatrix}$

Pembahasan

Menentukan matriks C.

C = A + B
   $=\begin{pmatrix} 8 & 3\\ 5 & 2 \end{pmatrix}+\begin{pmatrix} 6 & 4\\ 7 & 5 \end{pmatrix}$
   $=\begin{pmatrix} 14 & 7\\ 12 & 7 \end{pmatrix}$

Untuk menentukan invers dari matriks C, kita gunakan rumus

$Rumus invers matriks$

Berdasarkan rumus di atas, invers matriks C adalah:

$C^{-1}=\frac{1}{14\cdot 7-12\cdot 7}\begin{pmatrix} 7 & -7\\ -12 & 14 \end{pmatrix}$
         $=\frac{1}{14}\begin{pmatrix} 7 & -7\\ -12 & 14 \end{pmatrix}$
         $=\begin{pmatrix} \frac{1}{2} & -\frac{1}{2}\\ -\frac{6}{7} & 1 \end{pmatrix}$

Jadi, invers dari matriks C adalah opsi (E).

Soal No. 24 tentang Perkalian Matriks

Jika

$Soal perkalian matriks$

maka matriks P adalah ....

$\textrm{A. }\; \; \begin{pmatrix} 1 & 5\\ 1 & 4 \end{pmatrix}$
$\textrm{B. }\; \; \begin{pmatrix} -4 & 5\\ 1 & -1 \end{pmatrix}$
$\textrm{C. }\; \; \begin{pmatrix} 4 & -5\\ -1 & 1 \end{pmatrix}$
$\textrm{D. }\; \; \begin{pmatrix} 1 & -5\\ -1 & 4 \end{pmatrix}$
$\textrm{E. }\; \; \begin{pmatrix} 4 & 5\\ -1 & 1 \end{pmatrix}$

Pembahasan

Pada perkalian matriks berlaku

AX = B
   X = A^-1B

Berdasarkan rumus tersebut maka

$P=\begin{pmatrix} 2 & 7\\ -2 & 3 \end{pmatrix}^{-1}\begin{pmatrix} 1 & -3\\ -11 & 13 \end{pmatrix}$
     $P=\frac{1}{6+14}\begin{pmatrix} 3 & -7\\ 2 & 2 \end{pmatrix}\begin{pmatrix} 1 & -3\\ -11 & 13 \end{pmatrix}$
     $P=\frac{1}{20}\begin{pmatrix} 80 & -100\\ -20 & 20 \end{pmatrix}$
     $=\begin{pmatrix} 4 & -5\\ -1 & 1 \end{pmatrix}$

Jadi, matriks P adalah opsi (C).

Soal No. 25 tentang Barisan dan Deret Aritmetika

Diketahui suatu barisan aritmetika mempunyai suku ketiga adalah 10 dan suku keenam adalah 22. Suku ke-20 barisan tersebut adalah ....

A.   72
B.   74
C.   76
D.   78
E.   80

Pembahasan

Kita gunakan rumus

U_n = a + (n − 1)b

U₃ = a + 2b = 10
U₆ = a + 5b = 22
        —————— −
                3b = 12   (bawah dikurangkan atas)
                  b = 4

b = 4 → a + 2b = 10
                a + 8 = 10
                       a = 2

Nah, sekarang kita sudah dapat menentukan suku ke-20.

U_n = a + (n − 1)b
U₂₀ = 2 + (20 − 1)4
       = 2 + 80 − 4
       = 78

Jadi, Suku ke-20 barisan aritmetika tersebut adalah 78 (D).

Simak Pembahasan Soal Matematika IPS UN 2014 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

Tuesday, 9 February 2016