Pembahasan Matematika IPS UN 2014 No. 16 - 20

Pembahasan soal Matematika IPS Ujian Nasional tahun 2014 nomor 16 sampai dengan nomor 20 tentang:

• aplikasi sistem persamaan linear, 
• sistem pertidaksamaan linear, 
• nilai optimum sistem pertidaksamaan linear, 
• model matematika program linear, serta 
• penyelesaian program linear.

Soal No. 16 tentang Aplikasi Sistem Persamaan Linear

Wati membeli 4 donat dan 2 coklat seharga Rp6.000,00. Tari membeli 3 donat dan 4 coklat dengan harga Rp10.000,00. Andi membeli sebuah donat dan sebuah coklat dengan membayar Rp5.000,00. Uang kembali yang diterima Andi adalah ....

A.   Rp2.200,00
B.   Rp2.400,00
C.   Rp2.600,00
D.   Rp2.800,00
E.   Rp4.600,00

Pembahasan

Kita buat permisalan terlebih dahulu. 

x : donat 
y : coklat

Selanjutnya kita tentukan kalimat matematika sistem persamaan linear tersebut.

Wati : 4x + 2y = 6.000         .... (1)
Tari   : 3x + 4y = 10.000       .... (2)

Eliminasi persamaan (1) dan (2).

4x + 2y =   6.000 |×2|  8x + 4y = 12.000
3x + 4y = 10.000 |×1|  3x + 4y = 10.000
                                    ———————— −
                                            5x = 2.000 
                                              x = 400

Substitusi x = 400 pada salah satu persamaan, misal persamaan (1).

x = 400 →  4x + 2y =   6.000
                    4×400 + 2y = 6.000
                    1.600 + 2y = 6.000
                    2y = 4.400
                      y = 2.200

Dengan demikian, harga sebuah donat dan sebuah cokelat yang dibeli Andi adalah:

x + y = 400 + 2.200
          = 2.600

Uang kembali = 5.000 − 2.600
                      = 2.400

Jadi, uang kembalian Andi adalah  Rp2.400,00 (B).

Soal No. 17 tentang Sistem Pertidaksamaan Linear

Nilai maksimum dari fungsi objektif 2x + 3y yang memenuhi sistem pertidaksamaan 3x + 2y ≥ 12; x + y ≤ 5; x ≥ 0; dan y ≥ 0 adalah ....

A.   18
B.   15
C.   13
D.   12
E.   8

Pembahasan

Karena koefisien x dan y pada fungsi objektif nilainya hampir sama, dapat dipastikan nilai maksimum fungsi tersebut berada pada titik potong kedua garis yang membatasi sistem pertidaksamaan. Titik potong tersebut dapat kita tentukan dengan mengeliminasi kedua garis tersebut.

3x + 2y = 12   |×1|   3x + 2y = 12 
  x +   y =   5   |×2|   2x + 2y = 10
                              —————— −
                                           x = 2

Substitusi x = 2 ke salah satu persamaan. 

x = 2 →  x + y = 5
                2 + y = 5
                       y = 3

Substitusi x = 2 dan y = 3 ke fungsi objektif.

2x + 3y = 2×2 + 3×3
              = 4 + 9
              = 13

Jadi, nilai maksimum dari fungsi objektif tersebut adalah 13 (C).

Soal No. 18 tentang Nilai Optimum Sistem Pertidaksamaan Linear

Daerah yang diarsir pada gambar merupakan himpunan penyelesaian sistem pertidaksamaan.

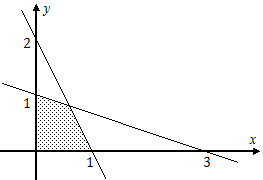
Nilai maksimum bentuk objektif 3x + 4y adalah ....

A.   3
B.   4
C.   5
D.   6
E.   7

Pembahasan

Sebagaimana nomor 17, koefisien x dan y pada fungsi objektifnya hampir sama besar. Berarti nilai maksimum fungsi objektif tersebut berada di titik yang menjauhi sumbu koordinat, yaitu berada di titik potong kedua garis.

Untuk menentukan persamaan garisnya, perhatikan ilustrasi berikut ini!

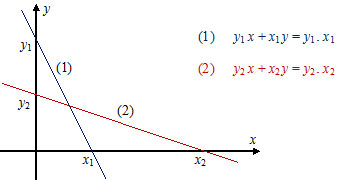
Berdasarkan ilustrasi di atas diperoleh

2x + y = 2 
x + 3y = 3

Sekarang kita eliminasikan kedua persamaan tersebut.

2x +   y = 2   |×3|   6x + 3y = 6 
  x + 3y = 3   |×1|     x + 3y = 3
                              —————— −
                                      5x = 3 
                                        x = 3/5 

x = 3/5 →  x + 3y = 3
               3/5 + 3y = 3
                        3y = 3 − 3/5
                             = 12/5 
                          y = 4/5

Substitusi nilai x dan y yang baru kita dapatkan ke fungsi objektif.

3x + 4y = 3 × 3/5 + 4 × 4/5
             =  9/5 + 16/5
             = 25/5
             = 5

Jadi, nilai maksimum bentuk objektif tersebut adalah 5 (C).

Soal No. 19 tentang Model Matematika Program Linear

Tempat parkir seluas 600 m² hanya mampu menampung 58 bus dan mobil. Tiap mobil membutuhkan tempat seluas 6 m² dan bus menempati 24 m². Model matematika yang memenuhi persamaan tersebut adalah ....

A.   x + y ≤ 58; x + 4y ≤ 100; x ≥ 0; y ≥ 0
B.   x − y ≤ 58; x + 4y ≤ 100; x ≥ 0; y ≥ 0
C.   x + y ≤ 58; x − 4y ≤ 100; x ≥ 0; y ≥ 0
D.   x + y ≤ 58; x + 4y ≥ 100; x ≥ 0; y ≥ 0
E.   x + y ≥ 58; x + 4y ≤ 100; x ≥ 0; y ≥ 0

Pembahasan

Kita misalkan terlebih dahulu. 

x : mobil 
y : bus

Daya tampung mobil dan bus hanya 58. Artinya, jumlah mobil dan bus maksimum 58. Maksimum 58 berarti sama dengan 58 atau kurang. 

x + y ≤ 58

Jumlah luas mobil dan bus tidak mungkin melebihi 600 m². Artinya harus kurang dari atau maksimal sama dengan 600 m².

6x + 24y ≤ 600, atau 
  x +   4y ≤ 100

Jumlah mobil dan bus tidak mungkin negatif. Harus positif atau minimal nol. 

x ≥ 0; y ≥ 0

Jadi, model matematika yang memenuhi adalah opsi (A).

Soal No. 20 tentang Penyelesaian Program Linear

Rombongan wisatawan yang terdiri dari 32 orang menyewa kamar hotel. Kamar yang tersedia adalah tipe A untuk 3 orang dan tipe B untuk 4 orang. Kamar tipe B yang disewa lebih banyak dari kamar tipe A, tetapi tidak lebih dari 3/2 banyak kamar tipe A. Jika setiap kamar terisi penuh, selisih banyak kamar tipe A dan tipe yang disewa adalah ....

A.   1
B.   4
C.   5
D.   9
E.   11

Pembahasan

Data-data yang bisa kita dapatkan dari soal adalah sebagai berikut:

3A + 4B ≤ 32     ... (1)
B > A                  ... (2)
B ≤ 3/2 A            ... (3)

Pertidaksamaan (3) perlu  kita ubah menjadi:

B ≤ 3/2 A ⇔ B − 3/2 A ≤ 0
                 ⇔ 2B − 3A ≤ 0
                 ⇔ −3A + 2B ≤ 0      ... (4)

Sekarang kita lakukan eliminasi pertidaksamaan (1) dan (4).

  3A + 4B ≤ 32
−3A + 2B ≤  0
—————— +
            6B ≤ 32 
              B ≤ 32/6
              B ≤ 5,33
              B = 5

B ≤ 5,33 berarti nilai bilangan bulat B paling besar adalah 5. Karena pada pertidaksamaan (2) B > A, maka kita tetapkan nilai B yang paling besar, yaitu 5.

Selanjutnya, kita tinggal melakukan substitusi B = 5 ke persamaan (1).

B = 5 →  3A + 4B = 32   (dijadikan persamaan)
              3A + 4×5 = 32
                3A + 20 = 32
                        3A = 12 
                          A = 4

Selisih jumlah kamar tipe A dan tipe B adalah

|A − B| = |4 − 5|
             = 1

Jadi, selisih banyak kamar tipe A dan tipe B yang disewa adalah 1 (A).

Simak Pembahasan Soal Matematika IPS UN 2014 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.