Pembahasan Matematika IPS UN 2014 No. 6 - 10

Pembahasan soal Matematika IPS Ujian Nasional 2014 nomor 6 sampai dengan nomor 10 tentang:

• logaritma, 
• titik potong fungsi kuadrat, 
• titik balik fungsi kuadrat, 
• grafik fungsi kuadrat, dan 
• komposisi fungsi.

Soal No. 6 tentang Logaritma

Nilai dari ²log 6 + ²log 4 − ²log 3 adalah ....

A.   6
B.   5
C.   4
D.   3
E.   2

Pembahasan

Karena bilangan pokoknya sama, yaitu 2, maka soal tersebut dapat diselesaikan dengan rumus 

^alog x + ^alog y = ^alog x.y 
^alog x − ^alog y = ^alog x/y

Dengan menggunakan dua tersebut diperoleh


                                           = ²log 8
                                           = ²log 2³
                                           = 3

Jadi, nilai dari bentuk logaritma tersebut adalah 3(D).

Soal No. 7 tentang Titik Potong Fungsi Kuadrat 

Diketahui fungsi kuadrat f(x) = 2x² + 5x − 3. Koordinat titik potong dengan sumbu x dan sumbu y berturut-turut adalah ....

A.   (−½, 0), (3, 0), dan (0,3)
B.   (−3, 0), (½, 0), dan (0,3)
C.   (−3, 0), (−½, 0), dan (0,−3)
D.   (−3, 0), (½, 0), dan (0,−3)
E.   (−½, 0), (3, 0), dan (0,−3)

Pembahasan

Titik potong pada sumbu x (y = 0) 

                 f(x) = 0
   2x² + 5x − 3 = 0
(2x − 1)(x + 3) = 0 
x = ½ atau x = −3

∴ koordinat titik potong: (½, 0) dan (−3, 0)

Titik potong pada sumbu y (x = 0) 

f(x) = 2x² + 5x − 3 
f(0) = −3

∴ koordinat titik potong: (0, −3)

Jadi, koordinat titik potong fungsi tersebut terhadap sumbu x dan sumbu y adalah opsi (D).

Soal No. 8 tentang Titik Balik Fungsi Kuadrat

Koordinat titik balik fungsi y = −2x² + 4x + 6 adalah ....

A.   (1, 8)
B.   (1, 12)
C.   (−1, 0)
D.   (−2, −10)
E.   (2, 6)

Pembahasan

Koordinat titik balik atau titik puncak terdiri dari sumbu simetri sebagai absis dan nilai balik sebagai ordinat. Sumbu simetri fungsi tersebut adalah


   

Sumbu simetri juga bisa dicari dengan cara menurunkan fungsi tersebut 

          y' = 0
−4x + 4 = 0
      −4x = −4 
          x = 1

Sedangkan untuk mendapatkan nilai balik, kita substitusikan x = 1 pada fungsi kuadrat tersebut. 

x = 1 → y = −2x² + 4x + 6
                 = −2×1² + 4×1 + 6
                 = −2 + 4 + 6
                 = 8

Jadi, koordinat titik balik fungsi tersebut adalah (1, 8) (A).

Soal No. 9 tentang Grafik Fungsi Kuadrat

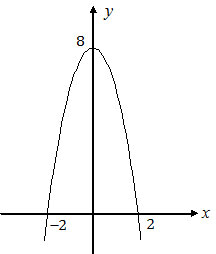
Persamaan grafik fungsi kuadrat pada gambar adalah ....

A.   y = 8 − x²
B.   y = 4 − x²
C.   y = 8 − 2x²
D.   y = 6 − 2x²
E.   y = 4 − 2x²

Pembahasan

Pada grafik di atas, kita dapatkan nilai pembuat nol fungsi, yaitu x₁ = −2 dan x₂ = 2. Untuk mendapatkan persamaannya, bisa kita gunakan rumus 

y = a(x − x₁)(x − x₂)
   = a(x + 2)(x − 2)
   = a(x² − 4)   ..... (1)

Nilai a bisa kita peroleh dengan substitusi titik puncak (0, 8) pada persamaan (1).

(0, 8) → y = a(x² − 4)
              8 = a(0² − 4)
              8 = −4a
              a = −2

Persamaan grafik fungsi tersebut adalah substitusi a = −2 pada persamaan (1). 

a = −2 → y = a(x² − 4)
                   = −2(x² − 4)
                   = −2x² + 8
                   = 8 − 2x²

Jadi, persamaan grafik fungsi kuadrat pada gambar di atas adalah y = 8 − 2x² (C).

Soal No. 10 tentang Komposisi Fungsi

Diketahui f : R → R dan g : R → R yang didefinisikan f(x) = x − 5 dan g(x) = x² − 3x − 4. Komposisi fungsi (g o f)(x) = ....

A.   x² − 3x − 9
B.   x² − 3x − 36
C.   x² − 13x − 14
D.   x² − 13x + 6
E.   x² − 13x + 36

Pembahasan

(g o f)(x) berarti yang kita pakai acuan adalah fungsi g. Sedangkan fungsi f kita masukkan ke fungsi g. 

    g(x) = x² − 3x − 4 
g[f(x)] = [f(x)]² − 3f(x) − 4
            = (x − 5)² − 3(x − 5) − 4
            = (x² − 10x + 25) − 3x + 15 − 4
            = x² − 13x + 36

Jadi, komposisi fungsi tersebut adalah x² − 13x + 36 (E).

Simak Pembahasan Soal Matematika IPS UN 2014 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.