Pembahasan Matematika IPS UN 2015 No. 11 - 15

Pembahasan soal Matematika IPS Ujian Nasional tahun 2015 nomor 11 sampai dengan nomor 15 tentang:

• penyelesaian persamaan kuadrat, 
• sifat akar persamaan kuadrat, 
• persamaan kuadrat, 
• pertidaksamaan kuadrat, dan 
• sistem persamaan linear.

Soal No. 11 tentang Penyelesaian Persamaan Kuadrat

Himpunan penyelesaian persamaan kuadrat x² − 2x − 15 = 0 adalah ....

A.   {−5, −3}
B.   {−5, 3}
C.   {−3, 5}
D.   {−2, 5}
E.   {3, 5}

Pembahasan

Cara yang sudah lazim dalam menyelesaikan persamaan kuadrat di atas adalah dengan cara pemfaktoran. 

x² − 2x − 15 = 0
(x + 3)(x − 5) = 0 
x = −3 atau x = 5

Jadi, himpunan penyelesaian persamaan kuadrat di atas adalah {−3, 5} (C).

Soal No. 12 tentang Sifat Akar Persamaan Kuadrat

Misalkan x₁ dan x₂ adalah akar-akar persamaan kuadrat x² − 10x + 3 = 0 maka nilai dari x₁²x₂ + x₁x₂² adalah ....

A.   −30
B.   −10
C.   3
D.   10
E.   30

Pembahasan

Dari persamaan kuadrat x² − 10x + 3 = 0 kita peroleh: 

a = 1 
b = −10 
c = 3

Penjumlahan dan perkalian akarnya adalah: 

x₁ + x₂ = −b/a
            = 10 

x₁ . x₂ = c/a
           = 3

Sekarang kita masuk ke pertanyaan: 

x₁²x₂ + x₁x₂² = x₁.x₂(x₁ + x₂)
                      = 3 . 10
                      = 30

Jadi, nilai yang dimaksud adalah 30 (E).

Soal No. 13 tentang Persamaan Kuadrat

Persamaan kuadrat yang akar-akarnya −½ dan 3 adalah ....

A.   x² − 5x + 3 = 0
B.   x² − 5x − 3 = 0
C.   2x² − 5x + 3 = 0
D.   2x² − 5x − 3 = 0
E.   2x² − 7x − 3 = 0

Pembahasan

Biasanya kita menyelesaikan persamaan kuadrat dengan pemfaktoran kemudian kita peroleh akar-akarnya, seperti soal nomor 11. Nah, sekarang kita melakukan hal yang sebaliknya, dari akar-akar yang diketahui kita kerjakan mundur hingga diperoleh persamaannya. 

x = −½ dan x = 3
  (2x + 1)(x − 3) = 0
2x² − 6x + x − 3 = 0
     2x² − 5x − 3  = 0

Jadi, persamaan kuadrat untuk akar-akar tersebut adalah 2x² − 5x − 3 = 0 (D).

Soal No. 14 tentang Pertidaksamaan Kuadrat

Himpunan penyelesaian real pertidaksamaan x² + 4x − 5 ≤ 0 adalah ....

A.   {x| −5 ≤ x ≤ 1, x ∈ R}
B.   {x| −1 ≤ x ≤ 5, x ∈ R}
C.   {x| −5 ≤ x ≤ −1, x ∈ R}
D.   {x| x ≤ −1 atau x ≥ 5, x ∈ R}
E.   {x| x ≤ −5 atau x ≥ 1, x ∈ R} 

Pembahasan

Karena tanda pertidaksamaannya ≤, jawabannya tidak mungkin opsi D dan E dengan catatan a > 0. Untuk memastikan, kita lakukan pemfaktoran. 

   x² + 4x − 5 ≤ 0
(x + 5)(x − 1) ≤ 0

Sampai di sini sudah bisa ditebak, jawabannya adalah opsi A karena pembuat nolnya x = −5 dan x = 1. Baiklah, agar lebih meyakinkan, kita buat garis bilangannya.

Jadi, daerah pertidaksamaan yang dimaksud terletak pada interval −5 ≤ x ≤ 1 (A).

Soal No. 15 tentang Sistem Persamaan Linear

Diketahui sistem persamaan linear:



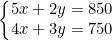
Nilai x adalah ....

A.   250
B.   200
C.   150
D.   100
E.   50

Pembahasan

Penyelesaian sistem persamaan linear yang paling umum adalah eliminasi. Karena yang ditanyakan nilai x maka yang harus dieliminasi adalah y.

5x + 2y = 850 |×3| 15x + 6y = 2550
4x + 3y = 750 |×2|   8x + 6y = 1500
                            ———————— −
                                        7x = 1050
                                          x = 150

Jadi, nilai x pada sistem persamaan linear tersebut adalah 150 (C).

Simak Pembahasan Soal Matematika IPS UN 2015 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.