Pembahasan Matematika IPS UN 2015 No. 16

Pembahasan soal Matematika IPS Ujian Nasional tahun 2015 nomor 16 sampai dengan nomor 20 tentang:

aplikasi sistem persamaan linear,
sistem pertidaksamaan linear,
program linear,
operasi matriks, dan
determinan matriks.

Soal No. 16 tentang Aplikasi Sistem Persamaan Linear

Ani dan Ina membeli bahan kue pada toko yang sama. Ani membeli 3 kg gula pasir dan 2 kg terigu seharga Rp52.000,00. Ina membeli 2 kg gula pasir dan 3 kg terigu seharga Rp48.000,00. Harga 3 kg terigu adalah ....

A. Rp18.000,00
B. Rp24.000,00
C. Rp28.000,00
D. Rp36.000,00
E. Rp38.000,00

Pembahasan

Kita buat permisalan dan model matematikanya

x : gula pasir
y : terigu

Ani : 3x + 2y = 52.000
Ina : 2x + 3y = 48.000

Harga 3 kg terigu: 3y = ?

Selanjutnya kita lakukan eliminasi. Karena yang ditanyakan terigu (y) maka yang perlu dieliminasi adalah x.

3x + 2y = 52.000 |×2| 6x + 4y = 104.000
2x + 3y = 48.000 |×3| 6x + 9y = 144.000
                                ————————— −
                                           5y = 40.000    (bawah dikurangi atas)
                                             y = 8.000

∴ 3y = 3 × 8.000
         = 24.000

Jadi, harga 3 kg terigu adalah Rp24.000,00 (B).

Soal No. 17 tentang Sistem Pertidaksamaan Linear

Nilai maksimum dari fungsi objektif f(x, y) = 3x + 2y pada daerah yang diarsir adalah ....

A. 15
B. 13
C. 12,5
D. 12
E. 10,5

Pembahasan

Koefisien x dan y pada fungsi objektif nilainya hampir sama, berarti nilai maksimum fungsi objektif tersebut berada di titik potong kedua garis. Persamaan kedua garis tersebut adalah

7x + 3,5y = 7×3,5
     2x + y = 7            .... (1)

5x + 5y = 5×5
    x + y = 5               .... (2)

Cara menentukan persamaan garis bisa di pelajari pada Pembahasan Matematika IPS UN 2014 No. 18.

Selanjutnya kita tentukan nilai x dan y melalui eliminasi persamaan (1) dan (2).

2x + y = 7
x + y = 5
————— −
        x = 2    → y = 3

∴ f(x, y) = 3x + 2y
     f(2, 3) = 3×2 + 2×3
          = 6 + 6
          = 12

Jadi, nilai maksimum fungsi objektif tersebut adalah 12 (D).

Soal No. 18 tentang Program Linear

Seorang pedagang akan berjualan kaos katun dan kaos nylon. Modal yang tersedia hanya Rp6.000.000,00. Harga beli kaos katun Rp20.000,00/potong dan kaos nylon Rp40.000,00/potong. Toko tersebut hanya mampu menampung tidak lebih dari 200 potong kaos. Keuntungan untuk setiap penjualan 1 potong kaos katun dan 1 potong kaos nylon berturut-turut adalah Rp3.000,00 dan Rp4.000,00. Keuntungan akan maksimal jika kaos katun terjual sebanyak ....

A. 50
B. 100
C. 125
D. 150
E. 200

Pembahasan

Kita gunakan tabel bantuan untuk mempermudah menentukan model matematikanya.

	Katun (x)	Nylon (y)	200
Harga Beli	~~20.000~~ 1	~~40.000~~ 2	~~6.000.000~~ 300
Keuntungan	3.000	4.000	-

Berdasarkan tabel bantuan tersebut diperoleh persamaan

x +   y = 200
x + 2y = 300

Keuntungan = 3000x + 4000y

Keuntungan maksimum terjadi di titik potong kedua garis tersebut. Hal ini karena koefisien x dan y hampir sama besar. Untuk menentukan titik potong dapat dilakukan dengan mengeliminasi kedua garis.

Karena yang ditanyakan kaos katun (x) maka y harus dieliminasi.

x +   y = 200 |×2| 2x + 2y = 400
x + 2y = 300 |×1|   x + 2y = 300
                                 ——————— −
                                      x = 100

Jadi, keuntungan maksimal akan tercapai jika kaos katun yang terjual sebanyak 100 potong (B).

Soal No. 19 tentang Operasi Matriks

Diketahui matriks

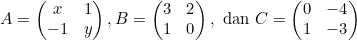
$A=\begin{pmatrix} x & 1\\ -1 & y \end{pmatrix},B=\begin{pmatrix} 3 & 2\\ 1 & 0 \end{pmatrix},\textrm{ dan }C=\begin{pmatrix} 0 & -4\\ 1 & -3 \end{pmatrix}$

Jika C^t adalah transpose matriks C maka nilai x − 2y yang memenuhi persamaan matriks 3A − B = C^t adalah ....

A. −2
B. −1
C. 0
D. 2
E. 3

Pembahasan

Kita selesaikan persamaan matriksnya terlebih dahulu.

                           3A − B = C^t
$\begin{pmatrix} 3x & 3\\ -3 & 3y \end{pmatrix}-\begin{pmatrix} 3 & 2\\ 1 & 0 \end{pmatrix}=\begin{pmatrix} 0 & 1\\ -4 & -3 \end{pmatrix}$
             $\begin{pmatrix} 3x-3 & 1\\ -4 & 3y \end{pmatrix}=\begin{pmatrix} 0 & 1\\ -4 & -3 \end{pmatrix}$

Kita sudah mendapatkan dua matriks yang sama. Berarti komponen yang bersesuaian juga sama. Sekarang kita ambil komponen kiri atas dan kanan bawah.

Kiri atas
3x − 3 = 0
      3x = 3
        x = 1

Kanan bawah
3y = −3
y = −1

Nah, sekarang masuk ke pertanyaan.

x − 2y = 1 − 2.(−1)
           = 1 + 2
           = 3

Jadi, nilai x − 2y sesuai dengan persamaan tersebut adalah 3 (E).

Soal No. 20 tentang Determinan Matriks

Diketahui matriks

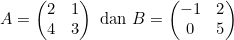
$A=\begin{pmatrix} 2 & 1\\ 4 & 3 \end{pmatrix}\textrm{ dan }B=\begin{pmatrix} -1 & 2\\ 0 & 5 \end{pmatrix}$

Determinan matriks A×B adalah ....

A. −10
B. −6
C. −2
D. 2
E. 10

Pembahasan

Cara pertama, kedua matriks tersebut dikalikan dulu kemudian ditarik determinannya.

$A\times B=\begin{pmatrix} 2 & 1\\ 4 & 3 \end{pmatrix}\times \begin{pmatrix} -1 & 2\\ 0 & 5 \end{pmatrix}$
             $=\begin{pmatrix} -2 & 9\\ -4 & 23 \end{pmatrix}$

det(A×B) = −2×23 − 9×(−4)    (ad − bc)
               = −46 + 36
               = −10

Cara kedua, masing-masing matriks ditarik determinan terlebih dahulu kemudian dikalikan.

det(A×B) = det A × det B
               = (6 − 4) × (−5 − 0)
               = 2 × (−5)
               = −10

Jadi, determinan matriks A×B adalah −10 (A).

Simak Pembahasan Soal Matematika IPS UN 2015 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 35
No. 16 - 20	No. 36 - 40

Dapatkan pembahasan soal dalam file pdf di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

Thursday, 18 February 2016