Pembahasan Matematika IPS UN 2018 No. 31 - 36

Pembahasan soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPS nomor 31 sampai dengan nomor 36 tentang:

• statistika [kuartil], 
• statistika [simpangan baku], 
• kaidah pencacahan [permutasi], 
• kaidah pencacahan [kombinasi], 
• teori peluang, dan 
• frekuensi harapan.

Soal No. 31 tentang Statistika [kuartil]

Perhatikan berat badan dari kelompok siswa!

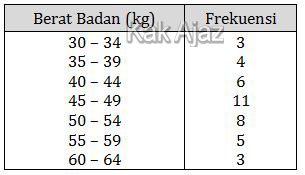
Kuartil dari berat badan siswa adalah ….

A.   37,00 kg
B.   42,00 kg
C.   45,50 kg
D.   53,25 kg
E.   53,78 kg

Pembahasan

Pada soal di atas, tidak disebutkan kuartil bawah atau kuartil atas. Kak Ajaz bahas keduanya saja, ya. Sekalian untuk belajar.

Jumlah data pada tabel adalah N = 40. Kuartil bawah (Q₁) terletak pada 1/4 N = 10, sedangkan kuartil atas (Q₃) terletak pada 3/4 N = 30.

Perhatikan cara menentukan besaran-besaran kuartil di bawah ini!

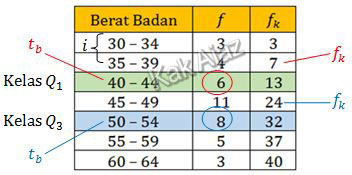
Kuartil bawah dirumuskan:

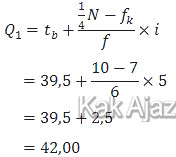
Sedangkan kuartil atas dirumuskan:

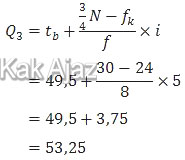
Jadi, jika yang ditanyakan kuartil bawah maka jawabannya adalah 42,00 (B). Tetapi jika yang ditanyakan kuartil atas maka jawabannya adalah 53,25 (D).

Soal No. 32 tentang Statistika [simpangan baku]

Simpangan baku dari data 7, 3, 4, 5, 6, 8, 2 adalah ….

A.   0
B.   1
C.   2
D.   5
E.   7

Pembahasan

Rata-rata data tersebut adalah: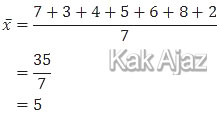

Simpangan baku dirumuskan sebagai:

Jadi, simpangan baku data tersebut adalah 2 (C).

Soal No. 33 tentang Kaidah Pencacahan [permutasi]

Dari 9 siswa akan dipilih 3 siswa untuk menjadi pengurus kelas yaitu sebagai ketua, sekretaris, dan bendahara kelas. Banyak susunan pengurus yang mungkin adalah ….

A.   84 susunan
B.   220 susunan
C.   405 susunan
D.   504 susunan
E.   1.320 susunan

Pembahasan

Karena ketiga pengurus tersebut kedudukannya berbeda (bertingkat) maka soal di atas bisa diselesaikan dengan permutasi, yaitu 9 permutasi 3.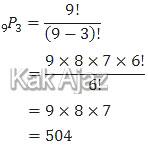

Jadi, banyak susunan pengurus yang mungkin adalah 504 susunan (D).

Soal No. 34 tentang Kaidah Pencacahan [kombinasi]

Seorang ibu akan memilih 4 bunga dari 8 macam bunga. Banyak cara yang mungkin untuk memilih bunga tersebut adalah ….

A.   24 cara
B.   32 cara
C.   70 cara
D.   1.680cara
E.   40.320 cara

Pembahasan

Empat bunga yang akan dipilih kedudukannya setara sehingga bisa dikerjakan dengan kombinasi, yaitu 8 kombinasi 4.

Jadi, banyak cara yang mungkin untuk memilih bunga tersebut adalah 70 cara (C).

Soal No. 35 tentang Teori Peluang

Sebuah dadu dan sebuah koin dilambungkan satu kali secara bersama-sama. Peluang muncul gambar pada koin dan bilangan genap pada dadu adalah ….

A.   1/4
B.   1/2
C.   2/3
D.   3/4
E.   6/7

Pembahasan

Semua kejadian yang mungkin bila sebuah dadu (bersisi 6) dan sebuah koin (bersisi 2) dilempar bersama-sama adalah:

n(S) = 6 × 2
        = 12

Misal A menyatakan muncul gambar pada koin dan bilangan genap pada dadu maka:

    A  :  (G, 2), (G, 4), (G, 6)
n(A) = 3

Dengan demikian, peluang kejadian A adalah:

p(A) = n(A)/n(S)
         = 3/12
         = 1/4

Jadi, peluang muncul gambar pada koin dan bilangan genap pada dadu adalah 1/4 (A).

Soal No. 36 tentang Frekuensi Harapan

Dua dadu dilambungkan secara bersama-sama sebanyak 360 kali. Frekuensi harapan muncul mata dadu berjumlah 7 adalah ….

A.   60 kali
B.   50 kali
C.   40 kali
D.   36 kali
E.   24 kali

Pembahasan

Banyak kejadian yang mungkin bila 2 dadu (bersisi 6) dilempar bersama-sama adalah:

n(S) = 6²
        = 36

Jika A menyatakan muncul mata dadu berjumlah 7 maka:

A : (1, 6), (2, 5), (3, 4), (4, 3), (5, 2). (6, 1)
n(A) = 6

Peluang kejadian A adalah:

p(A) = n(A)/n(S)
         = 6/36
         = 1/6

Frekuensi harapan kejadian A adalah peluang kejadian A dikalikan banyaknya pelemparan.

f_h(A) = p(A) × N
         = 1/6 × 360
         = 60

Jadi, frekuensi harapan muncul mata dadu berjumlah 7 adalah 60 kali (A).

Simak Pembahasan Soal Matematika IPS UN 2018 selengkapnya.

No. 01 - 05	No. 21 - 25
No. 06 - 10	No. 26 - 30
No. 11 - 15	No. 31 - 36
No. 16 - 20	No. 37 - 40

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.