Pembahasan Matematika No. 1 - 5 TKA Saintek UTBK SBMPTN 2019

Pembahasan soal Matematika Tes Kompetensi Akademik Sains dan Teknologi (TKA Saintek) Ujian Tulis Berbasis Komputer (UTBK) dalam Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2019 nomor 1 sampai dengan nomor 5 tentang:

• sistem persamaan, 
• pertidaksamaan, 
• persamaan kuadrat, 
• dimensi tiga, dan 
• bunga bank.

Soal No. 1 tentang Sistem Persamaan

Diketahui sistem persamaan

mempunyai solusi (x, y) dengan x dan y bilangan riil. Jumlah semua ordinatnya adalah ….

A.	−4
B.	−2
C.	0
D.	2
E.	4

Pembahasan

Eliminasi dari sistem persamaan tersebut adalah:

x2 + y2 + 2y − 8	=	0
x2 − y2 − 2y + 4x + 8	=	0
2x2 + 4x	=	0
x2 + 2x	=	0
x(x + 2)	=	0

x = 0 atau x = −2

Substitusi x = 0 dan x = −2 ke salah satu persamaan di atas, misal persamaan yang pertama.

x² + y² + 2y − 8 = 0

◈ Untuk x = 0

y² + 2y − 8 = 0

Misalkan akar-akarnya adalah y₁ dan y₂ maka penjumlahan akar-akarnya adalah:

y1 + y2	=	−b/a
	=	−2

◈ Untuk x = −2

4 + y2 + 2y − 8	=	0
y2 + 2y − 4	=	0

Misalkan akar-akarnya adalah y₃ dan y₄ maka penjumlahan akar-akarnya adalah:

y3 + y4	=	−b/a
	=	−2

Dengan demikian, jumlah semua ordinatnya adalah:

y1 + y2 + y3 + y4	=	−2 + (−2)
	=	−4

Jadi, jumlah semua ordinatnya adalah sistem persamaan tersebut adalah −4 (A).

Soal No. 2 tentang Pertidaksamaan

Himpunan penyelesaian pertidaksamaan ||x| + x| ≤ 2 adalah ….

A.	{x│0 ≤ x ≤ 1, x ∈ R}
B.	{x│x ≥ 0, x ∈ R}
C.	{x│x ≤ 2, x ∈ R}
D.	{x│x ≤ 0, x ∈ R}
E.	{x│x ≤ 1, x ∈ R}

Pembahasan

Perhatikan pertidaksamaan berikut!

||x| + x| ≤ 2

x yang pertama sudah pasti bernilai positif karena berharga mutlak sedangkan x yang kedua bisa bernilai positif atau negatif.

Jika x yang kedua bernilai positif maka:

x + x	≤	2
2x	≤	2
x	≤	1

Jika x yang kedua bernilai negatif maka:

x − x	=	2
0	=	2

Tidak ada nilai x yang bisa diambil.

Jadi, himpunan penyelesaian pertidaksamaan tersebut adalah {x│x ≤ 1, x ∈ R} (E).

Soal No. 3 tentang Persamaan Kuadrat

Parabola y = x² − 6x + 8 digeser ke kanan sejauh 2 satuan searah dengan sumbu x dan digeser ke bawah sejauh 3 satuan searah sumbu y. Jika parabola hasil pergeseran ini memotong sumbu x di x₁ dan x₂ maka x₁ + x₂ = ….

A.	8
B.	9
C.	10
D.	11
E.	12

Pembahasan

Persamaan parabola di atas setelah mengalami pergeseran (a, b) maka akan menjadi:

y − b = (x − a)² − 6(x − a) + 8

Parabola tersebut digeser ke kanan 2 satuan (a = 2) dan digeser ke bawah 3 satuan (b = −3) sehingga:

y + 3	=	(x − 2)2 − 6(x − 2) + 8
y + 3	=	x2 − 4x + 4 − 6x + 12 + 8
y + 3	=	x2 − 10x + 24
y	=	x2 − 10x + 21

Parabola hasil pergeseran ini memotong sumbu x.

y	=	0
x2 − 10x + 21	=	0

Dengan demikian penjumlahan akar-akarnya adalah:

x1 + x2	=	−b/a
	=	10

Jadi, nilai dari x₁ + x₂ adalah 10 (C).

Soal No. 4 tentang Dimensi Tiga

Diberikan balok ABCD.EFGH dengan DC = 12 cm. CG = 20 cm, dan BC = 18 cm. T adalah titik tengah AD. Jika α adalah sudut antara garis GT dengan bidang ABCD, cos⁡ α = ….

A.	3/5
B.	3/4
C.	4/5
D.	2/3
E.	5/6

Pembahasan

Perhatikan gambar di bawah ini!

Panjang CT bisa dicari dari segitiga CDT yang tegak lurus di D.

Sedangkan panjang GT dapat dicari dari segitiga GTC yang tegak lurus di C.

Sekarang perhatikan segitiga GTC!

Jadi, nilai dari cos⁡α adalah 3/5 (A).

Soal No. 5 tentang Bunga Bank

Andi menabung di bank dengan saldo awal A dengan sistem bunga majemuk. Tiga tahun kemudian saldonya menjadi B. Cici menabung di bank yang sama dengan saldo awal X. Saldo Cici 6 tahun kemudian 3 kali lebih banyak dari saldo akhir Andi. Besarnya saldo awal Cici adalah …

Pembahasan

Bungan majemuk selama n periode dirumuskan sebagai:

M_n = M₀ (1 + b)ⁿ

Saldo awal Andi adalah A dan 3 tahun kemudian menjadi B.

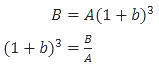
Saldo awal Cici adalah X dan 6 tahun kemudian menjadi 3 kali lebih banyak dari saldo akhir Andi.

3B = X(1 + b)⁶

Ok, sekarang kita selesaikan persamaan yang terakhir ini.

Jadi, besar saldo awal Cici adalah opsi (C).

Simak Pembahasan Soal TKA Saintek UTBK SBMPTN 2019 selengkapnya.

No. 01 - 05 (Mat)	No. 41 - 45 (Kim)
No. 06 - 10 (Mat)	No. 46 - 50 (Kim)
No. 11 - 15 (Mat)	No. 51 - 55 (Kim)
No. 16 - 20 (Mat)	No. 56 - 60 (Kim)
No. 21 - 25 (Fis)	No. 61 - 65 (Bio)
No. 26 - 30 (Fis)	No. 66 - 70 (Bio)
No. 31 - 35 (Fis)	No. 71 - 75 (Bio)
No. 36 - 40 (Fis)	No. 76 - 80 (Bio)

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.