Pembahasan Matematika No. 6 - 10 TKD Saintek 2014 Kode Naskah 512

Pembahasan soal Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2014 kode naskah 512 subtes Matematika nomor 6 sampai dengan nomor 10 tentang:

• limit fungsi, 
• eksponen, 
• integral tentu, 
• fungsi kuadrat, dan 
• lingkaran.

Soal No. 6 tentang Limit Fungsi

Jika lim_x→a [f(x) + 1/g(x)] = 4 dan lim_x→a [f(x) − 1/g(x)] = −3 maka lim_x→a [(f(x))² + 1/(g(x))²] = ....

A.   24/3
B.   23/5
C.   25/3
D.   25/2
E.   27/2

Pembahasan

Sifat limit yang harus diingat untuk menyelesaikan soal di atas adalah:

   lim_x→a [f(x) + g(x)]
= lim_x→a f(x) + lim_x→a g(x)

Berdasarkan sifat tersebut, maka:

   lim_x→a [f(x) + 1/g(x)]
= lim_x→a f(x) + lim_x→a 1/g(x) = 4     ...(1)

   lim_x→a [f(x) − 1/g(x)]
= lim_x→a f(x) − lim_x→a 1/g(x) = −3   ...(2)

Eliminasi persamaan (1) dan (2)

lim_x→a f(x) + lim_x→a 1/g(x) = 4
lim_x→a f(x) − lim_x→a 1/g(x) = −3
—————————————— −
                   2 lim_x→a 1/g(x) = 7
                      lim_x→a 1/g(x) = 7/2

Kita substitusikan hasilnya ke persamaan (1).

lim_x→a f(x) + lim_x→a 1/g(x) = 4
lim_x→a f(x) + 7/2 = 4
lim_x→a f(x) = 4 − 7/2
                   = 1/2

Selanjutnya kita masuk ke pertanyaan.

   lim_x→a [(f(x))² + 1/(g(x))²]
= lim_x→a (f(x))² + lim_x→a 1/(g(x))²
= (1/2)² + (7/2)²
= 1/4 + 49/4
= 50/4
= 25/2

Jadi, nilai limit tersebut adalah 25/2 (D).

Soal No. 7 tentang Eksponen

Nilai 𝑎 yang menyebabkan persamaan

9^𝑥 − 𝑎 ∙ 3^𝑥 + 𝑎 = 0

mempunyai tepat satu akar nyata adalah ….

A.   4
B.   0 atau 4
C.   𝑎 < 0
D.   𝑎 < 0 atau 4
E.   𝑎 < 0 atau 𝑎 > 4 

Pembahasan

Langkah pertama untuk menyelesaikan soal di atas adalah menyamakan bilangan pokoknya, yaitu 9^𝑥 = 3^2𝑥.

 9^𝑥 − 𝑎 ∙ 3^𝑥 + 𝑎 = 0
3^2𝑥 − 𝑎 ∙ 3^𝑥 + 𝑎 = 0

Selanjutnya kita misalkan 3^𝑥 = p sehingga diperoleh: 

p² − 𝑎p + 𝑎 = 0

Dari persamaan kuadrat ini diperoleh:

a = 1
b = −a
c = a 

Bentuk persamaan kuadrat ini mempunyai tepat satu akar nyata (sebagaimana pernyataan pada soal), padahal persamaan kuadrat seharusnya mempunyai dua akar. Berarti, kedua akar persamaan kuadrat tersebut nilainya sama, p₁ = p₂.

Agar persamaan kuadrat mempunyai akar kembar maka harus terpenuhi dua syarat. Pertama, nilai b (koefisien tengah) tidak sama dengan nol. Kedua, diskriminan persamaan kuadrat tersebut haruslah sama dengan nol. 

I.    b ≠ 0
    −a ≠ 0 
      a ≠ 0 

II.                  D = 0 
           b² − 4𝑎c = 0
    (−a)² − 4.1.𝑎 = 0
             a² − 4𝑎 = 0
            a(a − 4) = 0 
a = 0 (tidak memenuhi) atau a = 4

Jadi, nilai 𝑎 yang dimaksud adalah 4 (A).

Soal No. 8 tentang Integral Tentu

Jika 𝑓(𝑥) = 1 + sin 𝑥 + sin² 𝑥 + sin³ 𝑥 + ⋯, 0 ≤ 𝑥 ≤ 𝜋/4 maka _o∫^𝜋/4𝑓(𝑥) 𝑑𝑥 = ….

A.   −√2
B.   −1
C.   0
D.   1
E.   √2

Pembahasan

Fungsi f(x) merupakan jumlah deret geometri tak hingga dengan suku pertama a = 1 dan rasio r = sin x. 

f(x) = S_∞

     
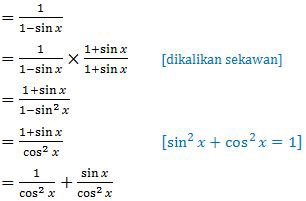
      = sec² x + tan x sec x

Sebelum masuk ke pertanyaan, ada dua rumus integral trigonometri yang harus kita ingat:

1. ∫ sec² x dx = tan x + C
2. ∫ tan x sec x dx = sec x + C

Sekarang kita selesaikan soal di atas. 

     _o∫^𝜋/4𝑓(𝑥) 𝑑𝑥
= _o∫^𝜋/4 (sec² x + tan x sec x) 𝑑x
= tan x + sec x ]_o^45°
= (tan 45° + sec 45°) − (tan 0° + sec 0°)
= (1 + √2) − (0 + 1)
= 1 + √2 − 1
= √2

Jadi, nilai integral fungsi f(x) adalah √2 (E).

Soal No. 9 tentang Fungsi Kuadrat

Diketahui suatu parabola simetris terhadap garis 𝑥 = −2 dan garis singgung parabola tersebut di titik (0, 1) sejajar garis 4𝑥 + 𝑦 = 4. Titik puncak parabola tersebut adalah ….

A.   (−2, −3)
B.   (−2, −2)
C.   (−2, 0)
D.   (−2, 1)
E.   (−2, 5)

Pembahasan

Misalkan fungsi parabola tersebut adalah 

y = ax² + bx + c

Titik singgung parabola adalah (0, 1). Berarti titik tersebut terletak pada parabola sehingga dapat disubstitusikan untuk mendapatkan nilai c.

(0, 1) → y = ax² + bx + c
              1 = a.0² + b.0 + c
              c = 1

Garis singgung parabola sejajar dengan garis 4𝑥 + 𝑦 = 4. Kita tentukan dulu gradien garis (m_g) dengan menggunakan rumus:

m_g = −a/b
      = −4/1
      = −4

Karena garis parabola sejajar dengan garis maka gradien garis singgung parabola (m_p) sama dengan gradien garis (m_g). 

m_p = m_g
      = −4

Sedangkan gradien parabola merupakan turunan fungsi parabola tersebut. 

m_p = y'
      = 2ax + b
 
Substitusi m_p = −4 dan absis titik singgung parabola (x = 0) pada gradien parabola, diperoleh:

−4 = 2a.0 + b
  b = −4

Parabola simetris terhadap garis x = 2 atau sumbu simetri adalah x = 2.

         x = −2
−b/(2a) = −2
  b/(2a) = 2
         b = 4a
       −4 = 4a
         a = −1

Dengan demikian, fungsi parabola tersebut adalah: 

y = −x² − 4x + 1

Nilai puncak parabola terjadi saat x = −2 (sumbu simetri). 

y = −(−2)² − 4(−2) + 1
   = −4 + 8 + 1
   = 5

Jadi, titik puncak parabola tersebut adalah (−2, 5) (E).

Soal No. 10 tentang Lingkaran

Jika lingkaran 𝑥² + 𝑦² − 2𝑎𝑥 + 𝑏 = 0 mempunyai jari-jari 2 dan menyinggung 𝑥 − 𝑦 = 0 maka nilai 𝑎² + 𝑏 adalah ….

A.   12
B.   8
C.   4
D.   2
E.   0

Pembahasan

Kita setarakan persamaan lingkaran di atas dengan bentuk umumnya.

𝑥² + 𝑦² − 2𝑎𝑥 + 𝑏 = 0
𝑥² + 𝑦² + A𝑥 + By + C = 0

Berdasarkan bentuk umum tersebut, diperoleh:

A = −2𝑎
B = 0
C = b
 
Pusat dan jari-jari lingkaran tersebut adalah:

pusat : (−½ A, −½B)   →  (a, 0)

jari-jari :  r² = ¼(A² + B²) − C
              2² = ¼[(−2𝑎)² + 0²] − b
                4 = 𝑎² − b     ..... (1)

Jarak titik pusat terhadap garis singgung lingkaran (𝑥 − 𝑦 = 0) merupakan jari-jari lingkaran tersebut.

 
 a = 2√2

Selanjutnya kita substitusikan a = 2√2 ke persamaan (1).

4 = 𝑎² − b
4 = (2√2)² − b
4 = 8 − b
b = 4

Dengan demikian,

𝑎² + 𝑏 = (2√2)² + 4
           = 8 + 4
           = 12

Jadi, nilai dari 𝑎² + 𝑏 adalah 12 (A).

Simak Pembahasan Soal TKD Saintek SBMPTN 2014 selengkapnya.

No. 01 - 05 (Mat)	No. 31 - 35 (Kim)
No. 06 - 10 (Mat)	No. 36 - 40 (Kim)
No. 11 - 15 (Mat)	No. 41 - 45 (Kim)
No. 16 - 20 (Fis)	No. 46 - 50 (Bio)
No. 21 - 25 (Fis)	No. 51 - 55 (Bio)
No. 26 - 30 (Fis)	No. 56 - 60 (Bio)

Dapatkan pembahasan soal dalam file pdf  di sini.

Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.