- eksponen,
- bentuk akar,
- logaritma,
- titik balik fungsi kuadrat, dan
- akar persamaan kuadrat.
Soal No. 1 tentang Eksponen
Diketahui p ≠ 0, q ≠ 0, dan r ≠ 0. Bentuk sederhana dari
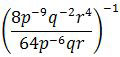
adalah ….
A. 2pqr
B. (3pqr)2
C. (2pqr)2
D. (2pqr−1)3
E. (2pqr−1)−3
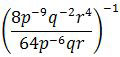
adalah ….
A. 2pqr
B. (3pqr)2
C. (2pqr)2
D. (2pqr−1)3
E. (2pqr−1)−3
Pembahasan
Langkah pertama untuk menyelesaikan soal di atas adalah mengubah pangkat negatif di luar kurung. Caranya tinggal menukar posisi pembilang dan penyebut.Dengan cara itu, pangkatnya menjadi 1. Pangkat 1 tidak perlu ditulis sehingga bentuk di atas menjadi:
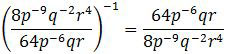
Dengan bentuk seperti ini, soal menjadi lebih ramah dan lebih bersemangat mengerjakannya.
Langkah berikutnya adalah menjumlah pangkat dari p, q, dan r. Jangan lupa, 64 dibagi dulu dengan 8. Diperoleh:
= 8 p−6+9 q1+2 r1−4
= 23 p3 q3 r−3
= (2pqr−1)3
Jadi, nilai dari bentuk pangkat tersebut adalah (2pqr−1)3 (D).
Soal No. 2 tentang Bentuk Akar
Bentuk sederhana dari (2√5 + 3√2)(6√5 − 2√2) adalah ….
A. 72 + 14√10
B. 72 − 22√10
C. 48 + 22√10
D. 48 + 14√10
E. 48 − 14√10
A. 72 + 14√10
B. 72 − 22√10
C. 48 + 22√10
D. 48 + 14√10
E. 48 − 14√10

Pembahasan
Mari kita kalikan masing suku pada soal di atas!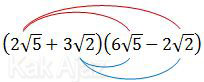
= 60 − 4√10 + 18√10 − 12
= 48 + 14√10
Jadi bentuk sederhana dari bentuk soal di atas adalah 48 + 14√10 (D).
Soal No. 3 tentang Logaritma
Nilai 3(2log y ) − 2log y2 + 2log (1/y) adalah ….
A. 1
B. 0
C. y
D. −1
E. −y
A. 1
B. 0
C. y
D. −1
E. −y
Pembahasan
Suku pertama kita ubah dengan menggunakan rumus:n alog x = alog xn
Sehingga soal di atas dapat diubah menjadi:
3(2log y ) − 2log y2 + 2log (1/y)
= 2log y3 − 2log y2 + 2log y−1
Karena bilangan pokoknya sama, yaitu 2, maka dapat diselesaikan dengan rumus:
alog x + alog y = alog x.y
alog x − alog y = alog (x/y)
Sehingga diperoleh:

Jadi, nilai dari bentuk logaritma di atas adalah 0 (B).
Soal No. 4 tentang Titik Balik Fungsi Kuadrat
Koordinat titik balik grafik fungsi f(x) = −2x2 − 4x + 5 adalah ….
A. (1, 5)
B. (−1, 5)
C. (−1, 7)
D. (1, 7)
E. (0, 5)
A. (1, 5)
B. (−1, 5)
C. (−1, 7)
D. (1, 7)
E. (0, 5)
Pembahasan
Dari fungsi f(x) = −2x2 − 4x + 5 diperoleh:a = −2
b = −4
c = 5
Koordinat titik balik merupakan titik pertemuan antara sumbu simetri dan nilai balik.
Sumbu simetri dapat dicari dengan rumus:
x = −b/(2a)
= −(−4)/[2(−2)]
= −(−4)/(−4)
= −1
Sehingga nilai balik terjadi saat x = −1.
y = f(−1)
= −2(−1)2 − 4(−1) + 5
= −2 + 4 + 5
= 7
Jadi, titik balik fungsi kuadrat tersebut adalah (−1, 7) (C).
Soal No. 5 tentang Akar Persamaan Kuadrat
Diketahui x1 dan x2 adalah akar-akar persamaan kuadrat x2 + 6x + 2 = 0. Nilai x12 + x22 − 4x1x2 adalah ….
A. 16
B. 18
C. 24
D. 26
E. 28
A. 16
B. 18
C. 24
D. 26
E. 28
Pembahasan
Dari persamaan kuadrat x2 + 6x + 2 = 0 diperoleh:a = 1
b = 6
c = 2
Penjumlahan kedua akar persamaan kuadrat tersebut adalah:
x1 + x2 = −b/a
= −6/1
= −6
Perkalian kedua akar persamaan kuadrat tersebut adalah:
x1 . x2 = c/a
= 2/1
= 2
Sebelum masuk ke pertanyaan, ingat rumus berikut ini!
x12 + x22 = (x1 + x2)2 − 2x1x2
Dengan demikian, soal di atas dapat diubah menjadi:
x12 + x22 − 4x1x2
= (x1 + x2)2 − 2x1x2 − 4x1x2
= (x1 + x2)2 − 6x1x2
Tujuan diubah ke bentuk tersebut agar diperoleh bentuk penjumlahan dan perkalian akar.
Sekarang kita substitusikan hasil penjumlahan dan perkalian akar persamaan kuadrat tersebut.
= (−6)2 − 6×2
=36 − 12
=24
Jadi, nilai x12 + x22 − 4x1x2 adalah 24 (C).
Simak Pembahasan Soal Matematika IPS UN 2016 selengkapnya.
| No. 01 - 05 | No. 21 - 25 |
| No. 06 - 10 | No. 26 - 30 |
| No. 11 - 15 | No. 31 - 35 |
| No. 16 - 20 | No. 36 - 40 |
Simak juga, Pembahasan Matematika IPS UN 2016 No. 01 - 05.
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

terima kasih
ReplyDeleteSama-sama
Delete